A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
WORK, ENERGY & POWER
DC PANDEY|Exercise Level 2 Subjective|15 VideosWORK, ENERGY & POWER
DC PANDEY|Exercise Level 2 Comprehension Based|2 VideosWORK, ENERGY & POWER
DC PANDEY|Exercise Level 2 objective|30 VideosWAVE MOTION
DC PANDEY|Exercise Integer Type Question|11 VideosWORK, ENERGY AND POWER
DC PANDEY|Exercise MEDICAL ENTRACES GALLERY|33 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-WORK, ENERGY & POWER-Level 2 More Than One Correct
- The potential energy of a particle of mass 5 kg moving in xy-plane is ...
Text Solution
|
- The potential energy of a particle is given by formula U=100-5x + 100x...
Text Solution
|
- One end of a light spring of spring constant k is fixed to a wall and ...
Text Solution
|
- Identify the correct statement about work energy theorem.
Text Solution
|
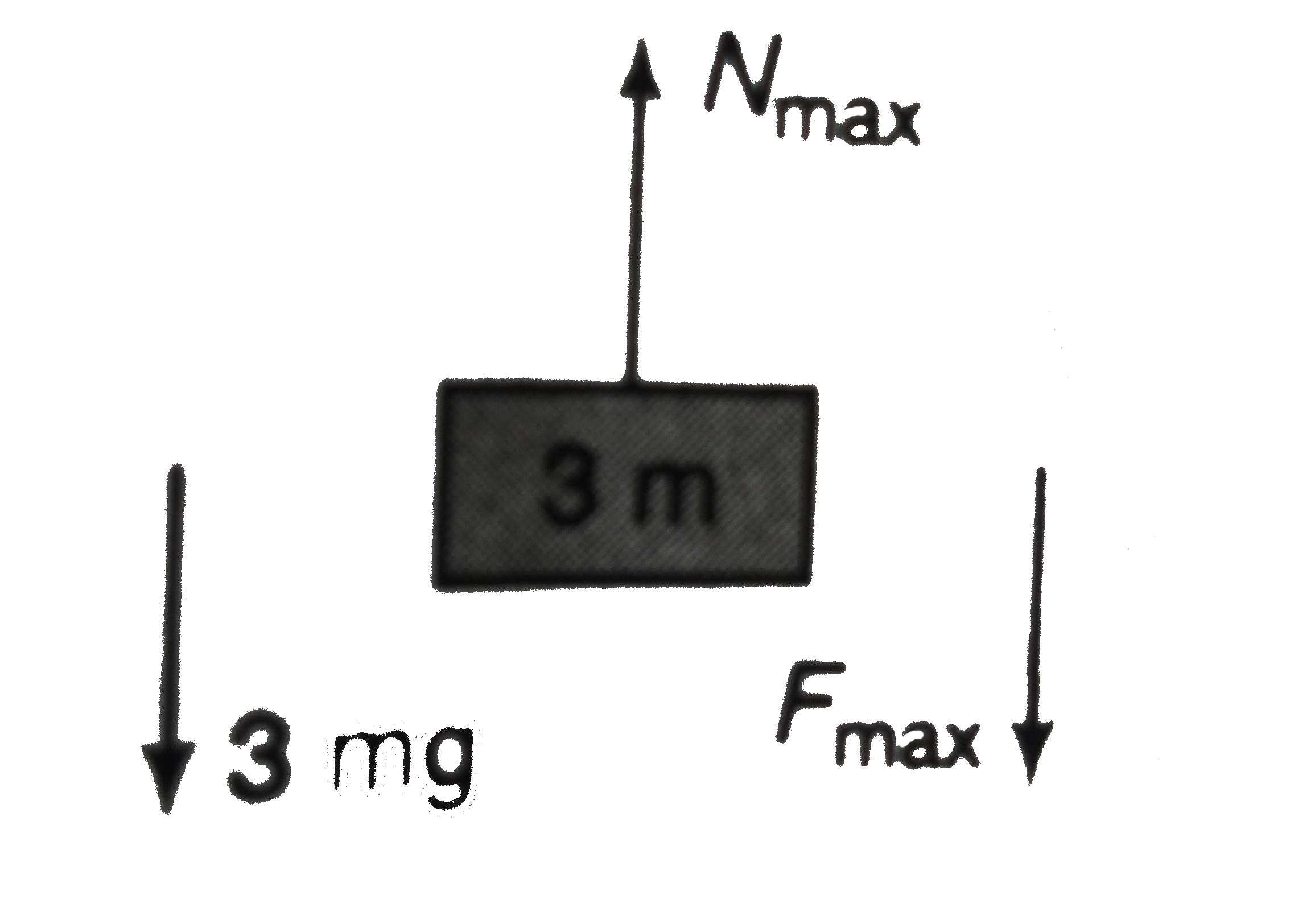
- A disc of mass 3 m and a dise of mass m are connected by a massless sp...
Text Solution
|
- In the adjoining figure, block A is of mass (m) and block B is of mass...
Text Solution
|
- If kinetic energy of a body is increasing then.
Text Solution
|
- At two positons kinetic energy and potential energy of a particle are ...
Text Solution
|
- Block A has no relative motion with resprct to wedge fixed to the lift...
Text Solution
|
 .
.