Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-GRAVITATION-Level 2 Subjective
- Three particle of mass m each are placed at the three corners of an eq...
Text Solution
|
- A man can jump vertically to a height of 1.5 m on the earth. Calculate...
Text Solution
|
- An artificial satellite is moving in a circular orbit around the earth...
Text Solution
|
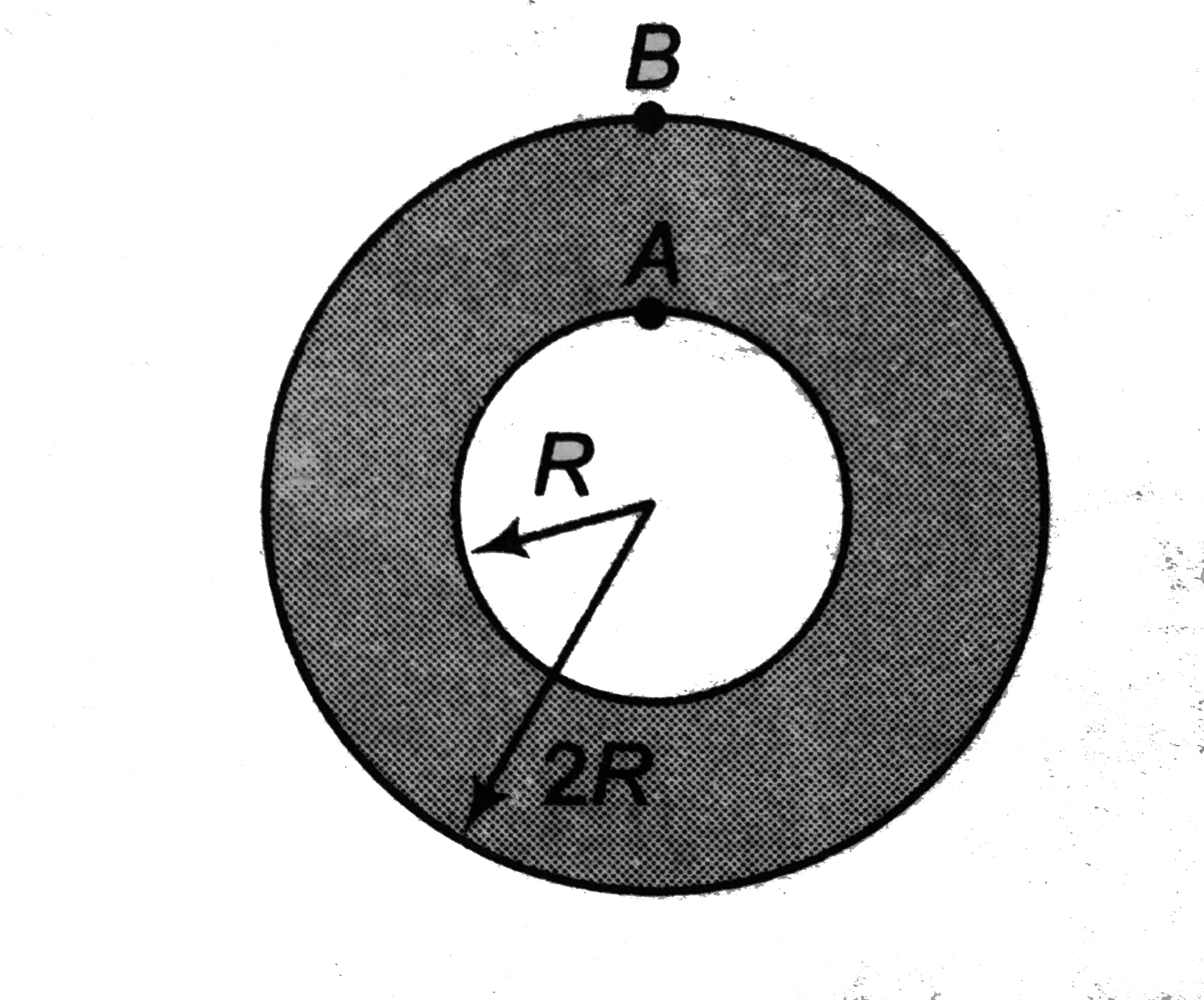
- A uniform metal sphere of radius R and mass m is surrounded by a thin ...
Text Solution
|
- Figure shows a spherical cavity inside a lead sphere. The surface of t...
Text Solution
|
- The density of the core a planet is rho(1) and that of the outer shell...
Text Solution
|
- If a satellite is revolving around a plenet of mass M in an elliptical...
Text Solution
|
- A uniform ring of mas m and radius a is placed directly above a unifor...
Text Solution
|
- Distance between the centres of two stars is 10a. The masses of these ...
Text Solution
|
- A smooth tunnel is dug along the radius of earth that ends at centre. ...
Text Solution
|
- Inside a fixed sphere of radius R and uniform density rho, there is sp...
Text Solution
|
- A ring of radius R = 4m is made of a highly dense material. Mass of th...
Text Solution
|
- Two planets of equal mass orbit a much massive star (figure). Planet m...
Text Solution
|
- In a double star, two stars one of mass m(1) and another of mass m(2),...
Text Solution
|