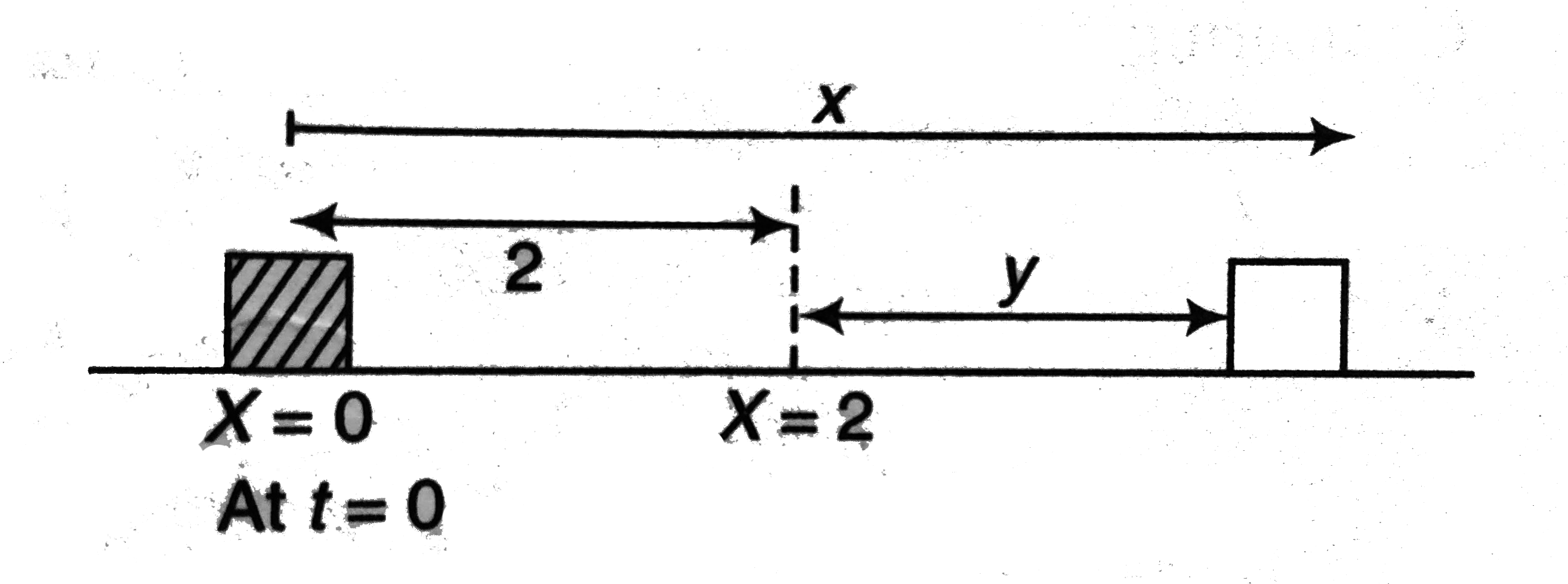
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
DC PANDEY|Exercise Level 1 Single Correct|24 VideosSIMPLE HARMONIC MOTION
DC PANDEY|Exercise Level 1 Subjective|39 VideosSIMPLE HARMONIC MOTION
DC PANDEY|Exercise Miscellaneous Examples|8 VideosSEMICONDUCTORS AND ELECTRONIC DEVICES
DC PANDEY|Exercise More than One Option is Correct|3 VideosSOLVD PAPERS 2017 NEET, AIIMS & JIPMER
DC PANDEY|Exercise Solved paper 2018(JIPMER)|38 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-SIMPLE HARMONIC MOTION-Level 1 Assertion And Reason
- Assertion : In x = A cos omega t, x is the displacement measured from ...
Text Solution
|
- Assertion : Aparticle is under SHM along the x - axis. Its mean positi...
Text Solution
|
- Assertion : A spring block system is kept over a smooth surface as sho...
Text Solution
|
- Assertion : Time taken by a particle in SHM to move from x = A to x = ...
Text Solution
|
- Assertion : Path of a particle in SHM is always a straight line. Rea...
Text Solution
|
- Assertion : In spring block system if length of spring and mass of blo...
Text Solution
|
- Assertion : All small oscillation are simple harmonic in nature. Rea...
Text Solution
|
- Assertion : In x = A cos omega t, the dot product of acceleration and...
Text Solution
|
- Assertion : For a given simple harmonic motion displacement (from the ...
Text Solution
|
- Assertion : We can call circular motion also as simple harmonic motion...
Text Solution
|