Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-FLUID MECHANICS-Miscellaneous Examples
- A ball of volume V and density rho(1) is moved downwards by a distance...
Text Solution
|
- In the figure shown find the value of h(2) for maximum range R if ...
Text Solution
|
- In the figure shown, find the range R.
Text Solution
|
- In the figure show, find v, t(op) and R.
Text Solution
|
- Figure shown a hydraulic press with the larger piston if diameter 35 c...
Text Solution
|
- A glass full of water upto a height of 10 cm has a bottom of are 10 cm...
Text Solution
|
- A soild ball of density half that of water falls freely under gravity ...
Text Solution
|
- A fresh water on a reservoir is 10m deep. A horizontal pipe 4.0 cm in ...
Text Solution
|
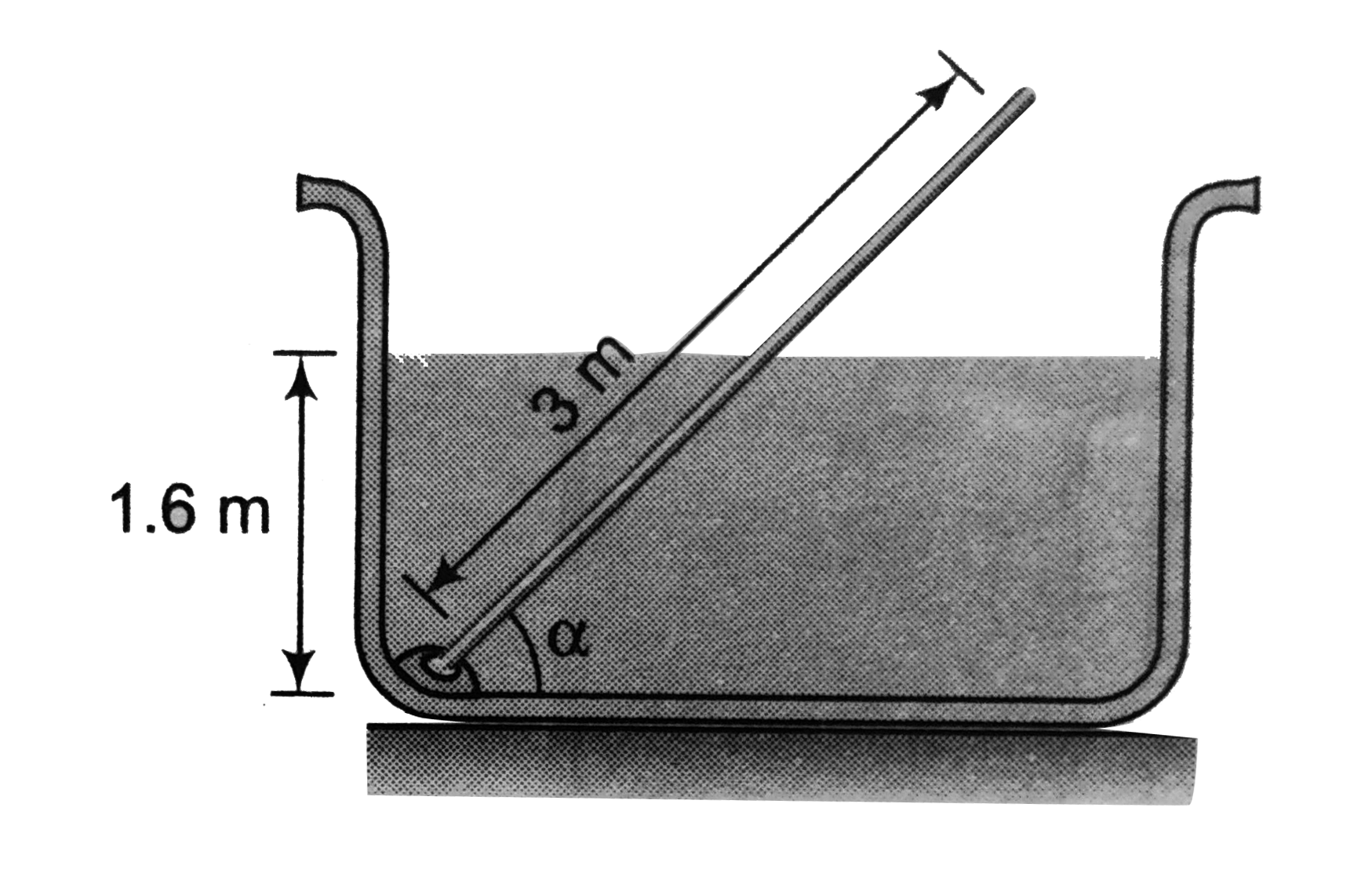
- A wooden rod weighing 25N is mounted on a hinge below the free surface...
Text Solution
|
- A cylindrical tank has a small hole at bottom. At t = 0, a tap starts ...
Text Solution
|
 .
.