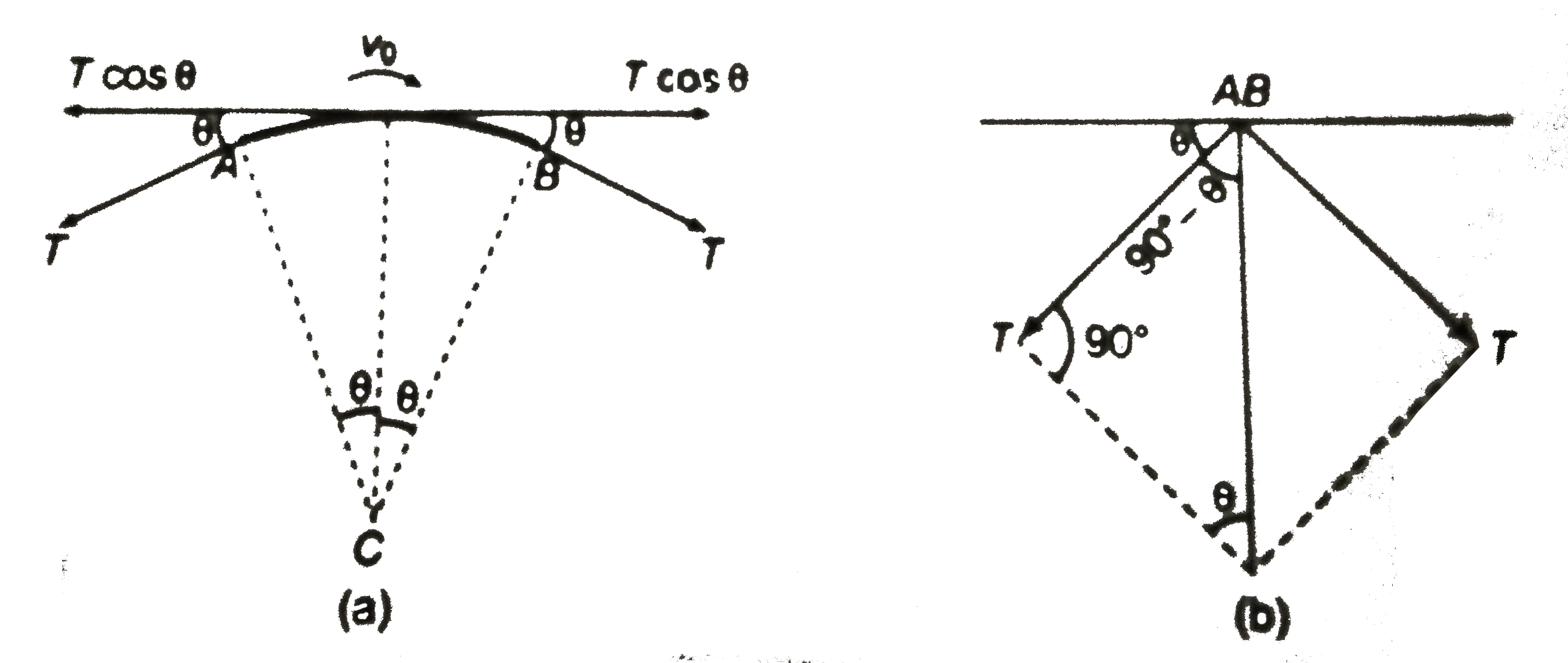
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-WAVE MOTION-Miscellaneous Examples
- A block of mass M = 2kg is suspended from a string AB of mass 6 kg as...
Text Solution
|
- A wave moves with speed 300 m//s on a wire which is under a tension of...
Text Solution
|
- For a wave described by y = A sin (omegat - kx), consider the followin...
Text Solution
|
- A thin string is held at one end and oscillates so that, y(x = 0, t...
Text Solution
|
- Consider a wave propagating in the negative x-direction whose frequenc...
Text Solution
|
- A simple harmonic wave of amplitude 8 units travels along positive x-a...
Text Solution
|
- A wave pulse on a horizontal string is represented by the function y...
Text Solution
|
- A uniform circular hoop of string is rotating clockwise in the absence...
Text Solution
|
- A sinusoidal wave trsvelling in the positive direction on a stretched ...
Text Solution
|