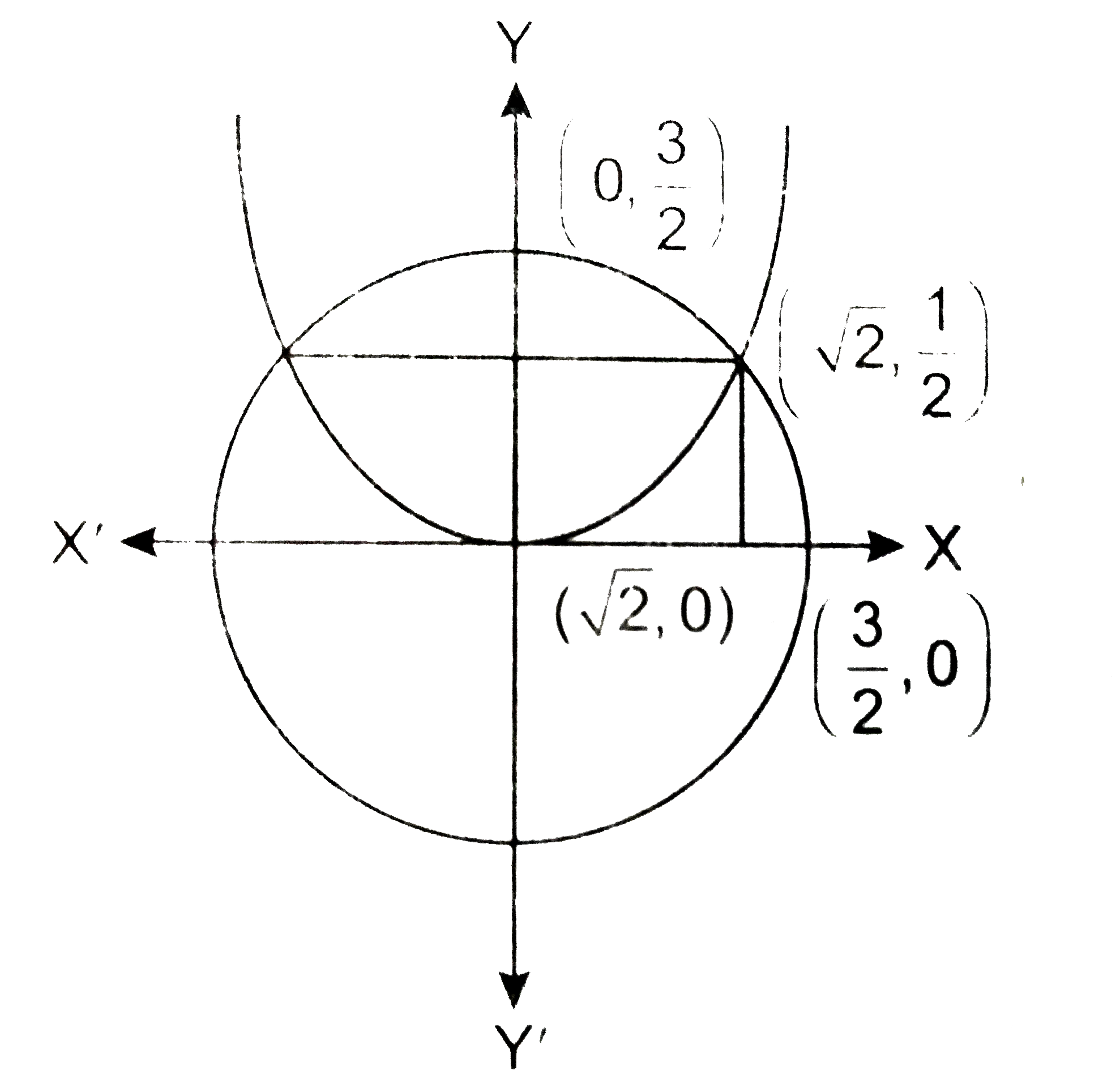लिखित उत्तर
Verified by Experts
NOOTAN HINDI-समाकलनो के अनुप्रयोग -प्रश्नावली 8.2
- परवलय x^(2) = 4y और वृत्त 4x^(2) + 4y^(2) = 9 के मध्यवर्ती क्षेत्र क...
Text Solution
|
- वक्रो (x -1)^(2) + y = 1 एव x^(2) + y^(2) =1 से घिरे क्षेत्र का क्षे...
Text Solution
|
- वक्रो y =x^(2) + 2,y=x ,x =0 एव x = 3 से घिरे क्षेत्र का क्षेत्रफ...
Text Solution
|
- समाकलन का उपयोग करते हुए एक ऐसे त्रिभुज का क्षेत्रफल ज्ञात कीजि...
Text Solution
|
- समाकलन का उपयोग करते हुए एक ऐसे त्रिकोणीय क्षेत्र का क्षेत्रफल ज्ञात क...
Text Solution
|
- वृत्त x^(2) + y^(2) = 4 एव रेखा x + y = 2 से घिरे छोटे भाग का ...
Text Solution
|
- वक्रो y^(2) = 4x एव y = 2x में मध्यवर्ती क्षेत्र का क्षेत्रफल है :
Text Solution
|