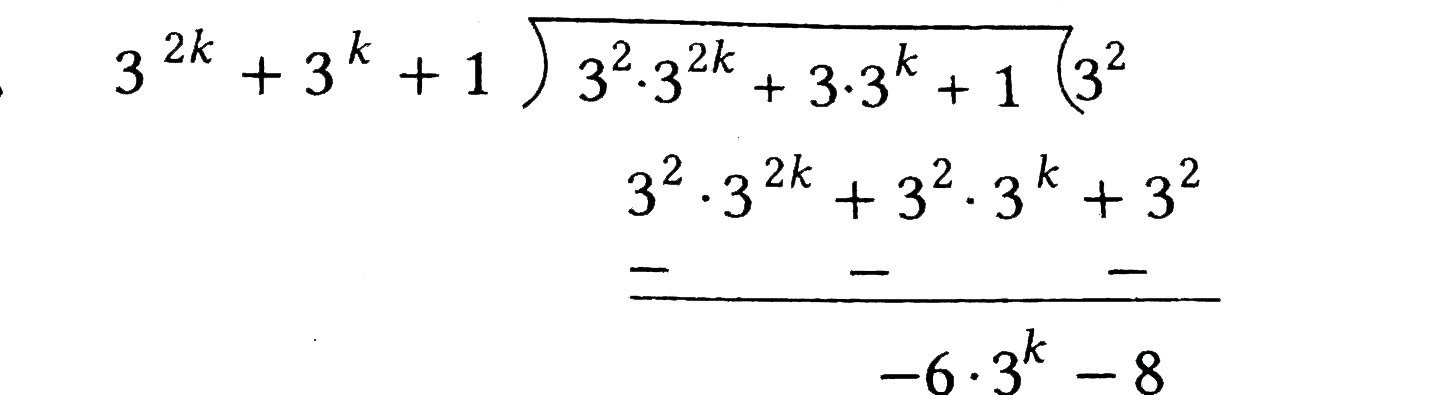Text Solution
Verified by Experts
Topper's Solved these Questions
MATHEMATICAL INDUCTION
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|2 VideosMATHEMATICAL INDUCTION
ARIHANT MATHS|Exercise Exercise (Statement I And Ii Type Questions)|3 VideosLOGARITHM AND THEIR PROPERTIES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|4 VideosMATRICES
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|49 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-MATHEMATICAL INDUCTION -Exercise (Subjective Type Questions)
- Prove the following by the principle of mathematical induction:\ 11...
Text Solution
|
- n^7-n is divisible by 42 .
Text Solution
|
- 3^(2n)+24n-1 is divisible by 32 .
Text Solution
|
- prove using mathematical induction:-n(n+1)(n+5) is divisible by 6 for ...
Text Solution
|
- Prove that (25)^(n+1)-24n+5735 is divisible by (24)^2 for all n=1,2,
Text Solution
|
- x^(2n-1)+y^(2n-1) is divisible by x+y
Text Solution
|
- Prove by induction that if n is a positive integer not divisible by 3....
Text Solution
|
- prove that the product of three consecutive positive integers is divis...
Text Solution
|
- Prove by induction that the sum of the cubes of three consecutive n...
Text Solution
|
- When the square of any odd number, greater than 1, is divided by 8,...
Text Solution
|
- Prove the following by using iduction for all n in N. 1+2+3+.....+n=(...
Text Solution
|
- 1^2+2^2+3^2++n^2=(n(n+1)(2n+1))/6
Text Solution
|
- 1.3+3.5+5.7+......+(2n-1)(2n+1)=(n(4n^2+6n-1))/3
Text Solution
|
- Prove the following by the principle of mathematical induction:1/(2...
Text Solution
|
- Prove 1.4.7+2.5.8+3.6.9+....... upto n terms =(n)/(4)(n+1)(n+6)(n+7)
Text Solution
|
- 1^2/(1.3)+2^2/(3.5)+3^2/(5.7)+.....+n^2/((2n-1)(2n+1))=((n)(n+1))/((2(...
Text Solution
|
- Let a(0)=2,a1=5 and for n ge 2, an=5a(n-1)-6a(n-2), then prove by indu...
Text Solution
|
- If a(1)=1,a(n+1)=(1)/(n+1)a(n),a ge1, then prove by induction that a(n...
Text Solution
|
- if a,b,c,d,e and f are six real numbers such that a+b+c=d+e+f a^2+b^2...
Text Solution
|
- Prove that tan^(- 1)(1/3)+tan^(- 1)(1/7)+tan^(- 1)(1/13)+..........+ta...
Text Solution
|