Text Solution
Verified by Experts
Topper's Solved these Questions
SOLID STATE
CENGAGE CHEMISTRY|Exercise Solved Examples|13 VideosSOLID STATE
CENGAGE CHEMISTRY|Exercise Exercises (Linked Comprehension)|13 VideosREDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDS
CENGAGE CHEMISTRY|Exercise SUBJECTIVE TYPE|3 VideosSOLUTIONS
CENGAGE CHEMISTRY|Exercise Ex 2.3 (Objective)|9 Videos
Similar Questions
Explore conceptually related problems
CENGAGE CHEMISTRY-SOLID STATE-Ex 1.2 (Objective)
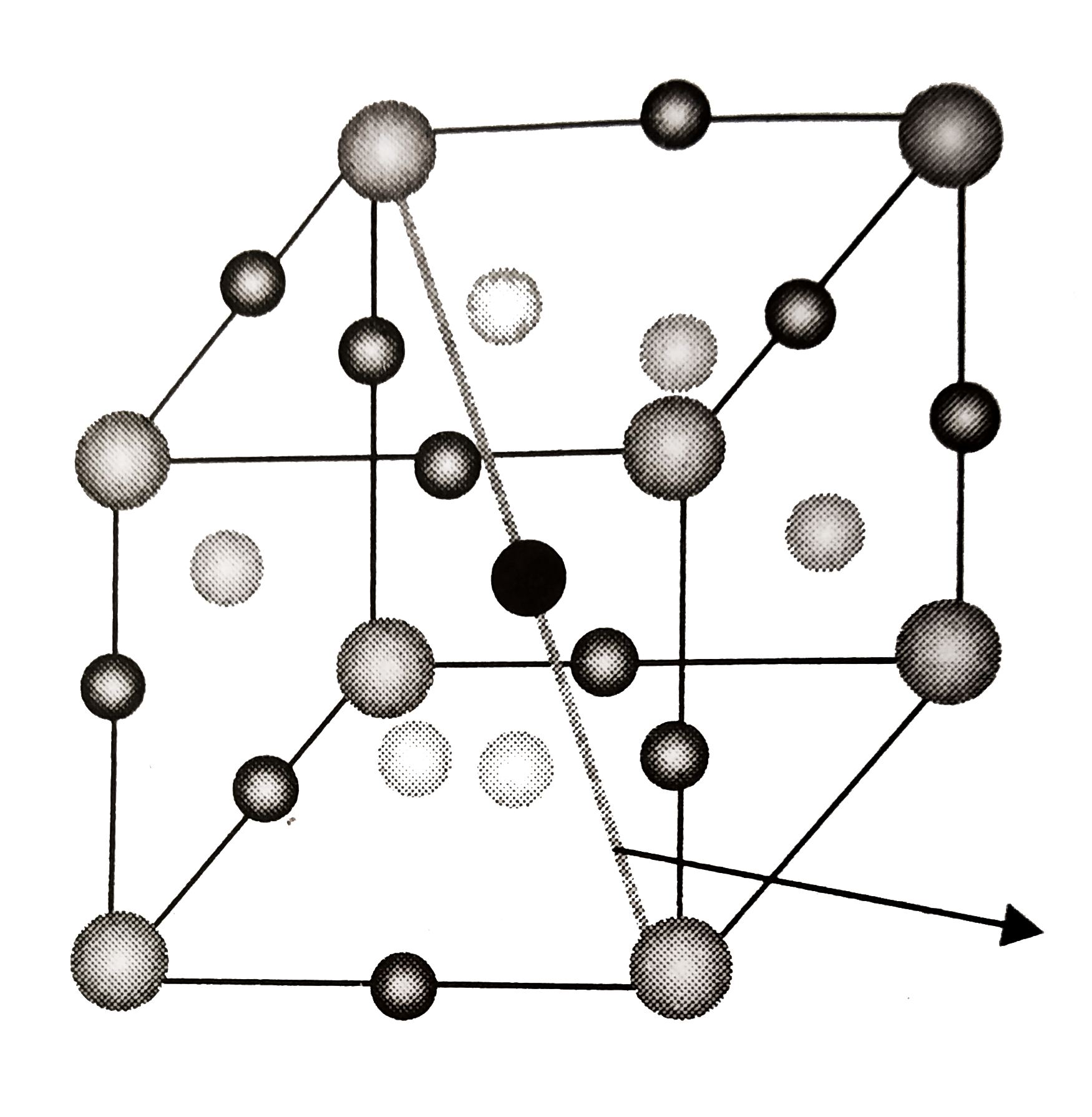
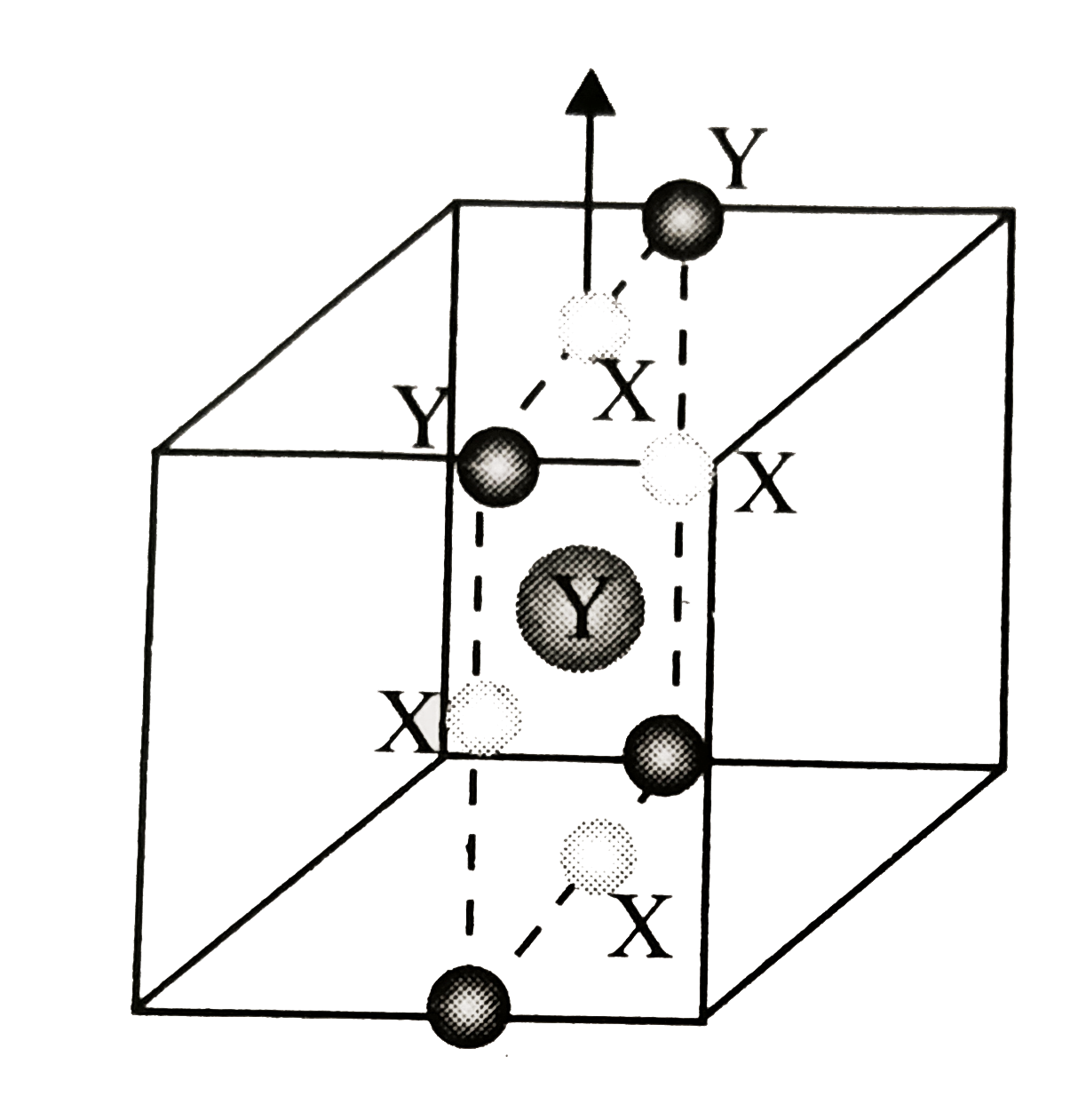
- A compound formed by elements X and Y has a cubic structure in which X...
Text Solution
|
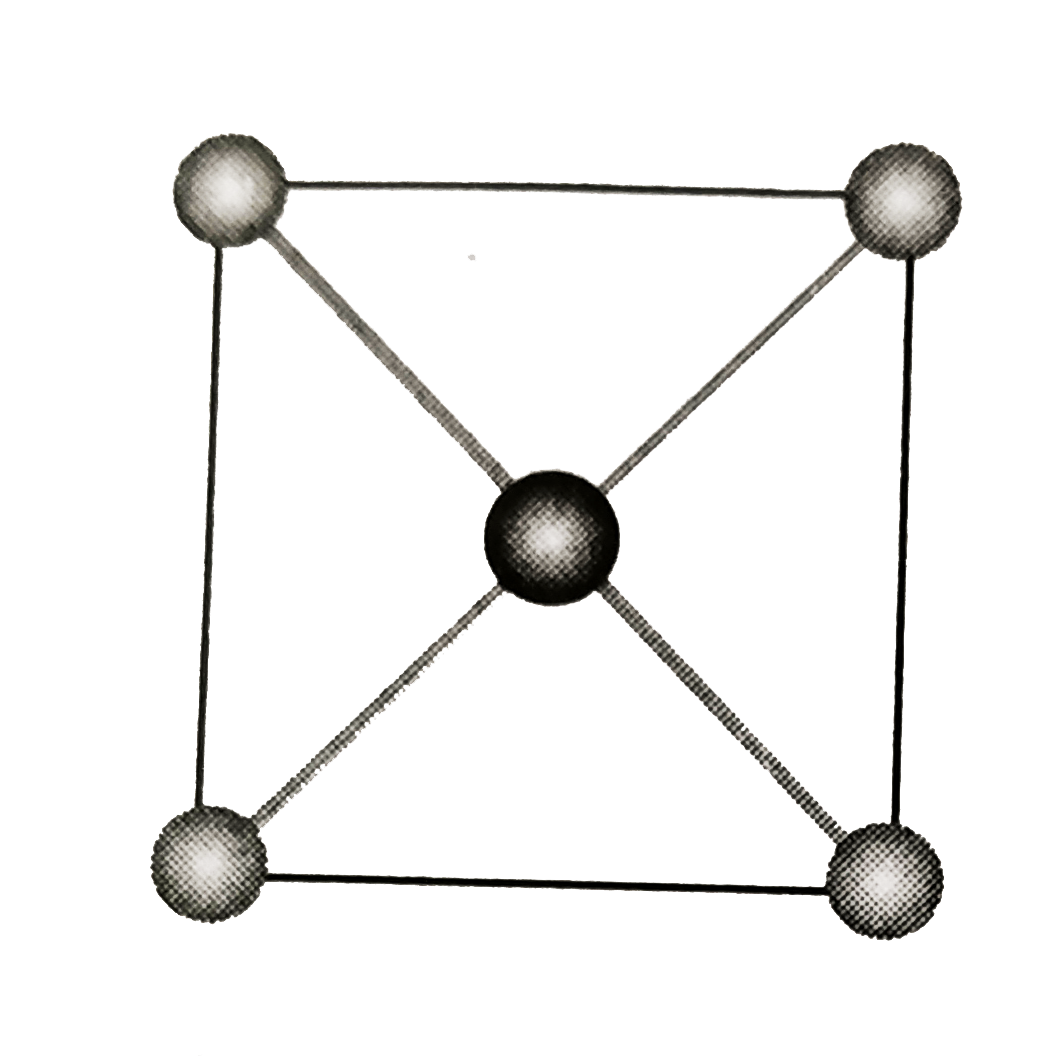
- The structure shown here represents
Text Solution
|
- The structure shwon here represents
Text Solution
|
- In AgCl, the Ag^(o+) ions are deisplaced from their lattice position t...
Text Solution
|
- NaCl shows Schottky defects and AgCl shows Frekel defects. Their elect...
Text Solution
|
- Amorphous solids are classified as
Text Solution
|
- Due of Frenkel defect
Text Solution
|
- Which of the following statement is//are correct?
Text Solution
|
- Which of the following statement is//are correct?
Text Solution
|
- Which of the following statement is//are correct?
Text Solution
|