Text Solution
Verified by Experts
Topper's Solved these Questions
SIMILARITY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise 2.5 (4 mark each)|3 VideosSIMILARITY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLE TYPE|50 VideosSIMILARITY
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise 2.3 (2 mark each)|10 VideosQUADRATIC EQUATIONS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNEMENT 2.4|8 VideosSTATISTICS
NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE (MCQs)|35 Videos
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-SIMILARITY-2.4 (3 mark each)
- Two triangles are similar. The lengths of the sides of the smaller tri...
Text Solution
|
- In DeltaABC, seg BD bisects /ABC. If AB=x, BC=x+5, AD=x-2, DC=x+2. Fin...
Text Solution
|
- In the figure X is any point in the interior of triangle. Point X is j...
Text Solution
|
- In DeltaABC, AP |BC, BQ|AC. B-P-C,A-Q-C, then prove that DeltaCPA~De...
Text Solution
|
- In the figure in DeltaABC, point D on side BC is such that /BAC=/ADC. ...
Text Solution
|
- In the figure, PS=3, SQ=6, QR=5, PT=x and TR=y. Give any two pairs of ...
Text Solution
|
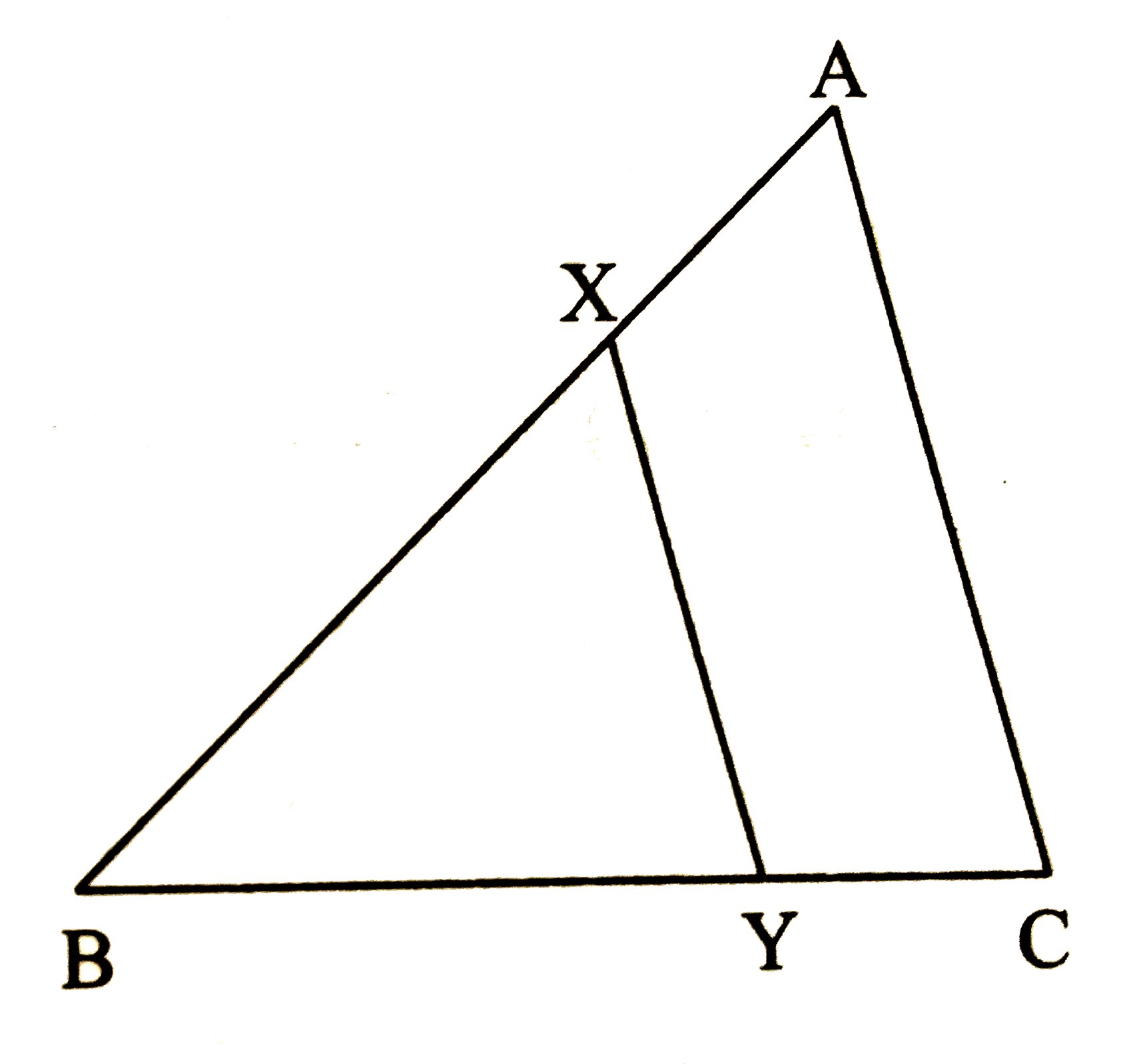
- In the adjoining figure, seg XY|| seg AC, IF 3AX=2BX and XY=9 then fin...
Text Solution
|
- In trapezium PQRS, side PQ|| side SR, AR=5AP, AS=5AQ then prove that S...
Text Solution
|