Text Solution
Verified by Experts
Topper's Solved these Questions
NEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Exercise 6.1|11 VideosNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Exercise 6.2|35 VideosNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Integer|5 VideosMISCELLANEOUS VOLUME 2
CENGAGE PHYSICS|Exercise INTEGER_TYPE|10 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS|Exercise Integer type|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 1-Solved Examples
- Two blocks of masses 5kg and 2 kg are initially at rest on the floor. ...
Text Solution
|
- In the arrangement shown in fig. m(1)=1kg, m(2)=2 kg. Pulleys are mass...
Text Solution
|
- Pulleys shown in the system are massless and fricionless. Threads are ...
Text Solution
|
- In the arrangement shown in fig., mass of the rod M exceeds the mass m...
Text Solution
|
- A block of mass m is placed on the inclined sufrace of a wedge as show...
Text Solution
|
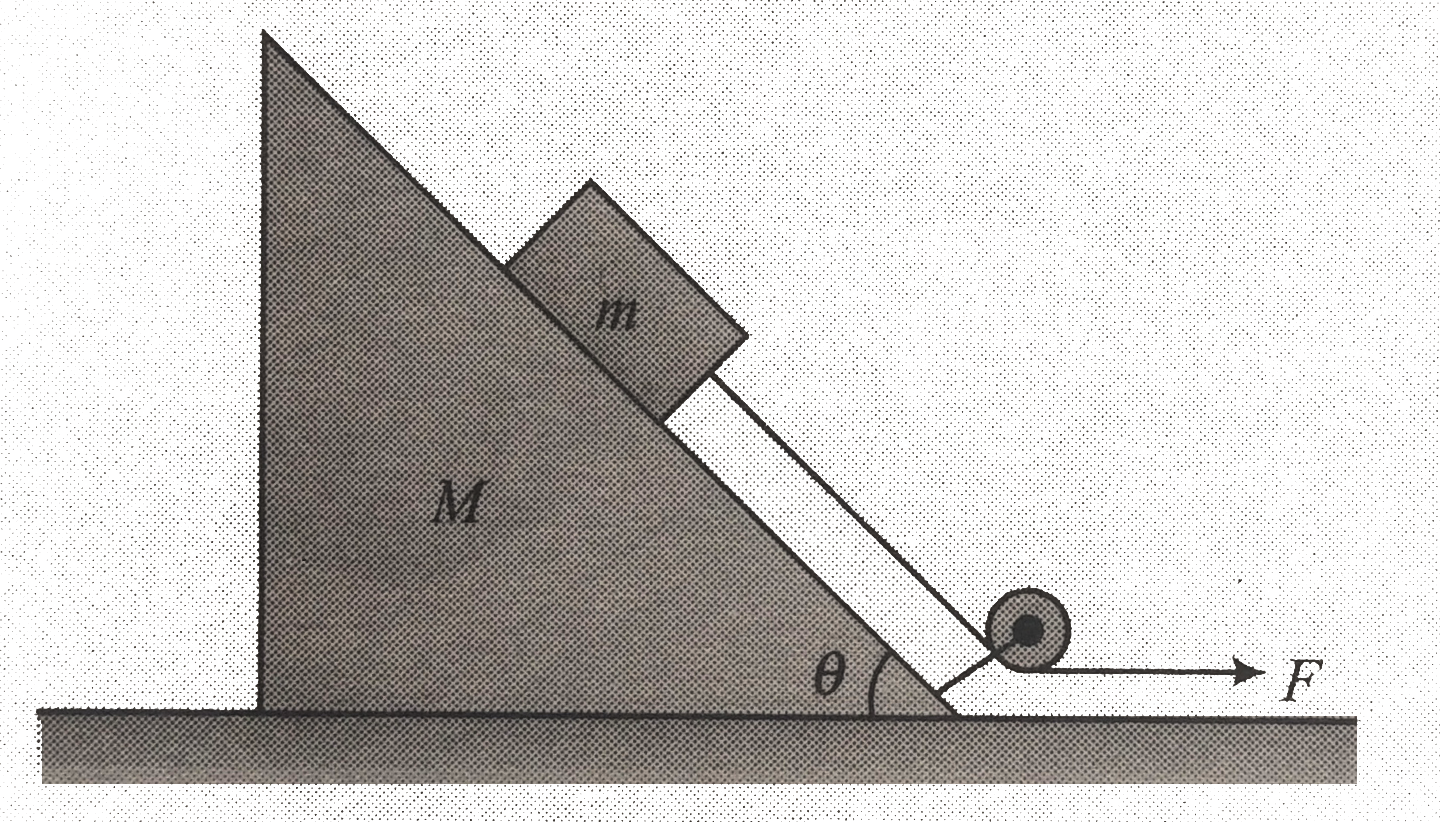
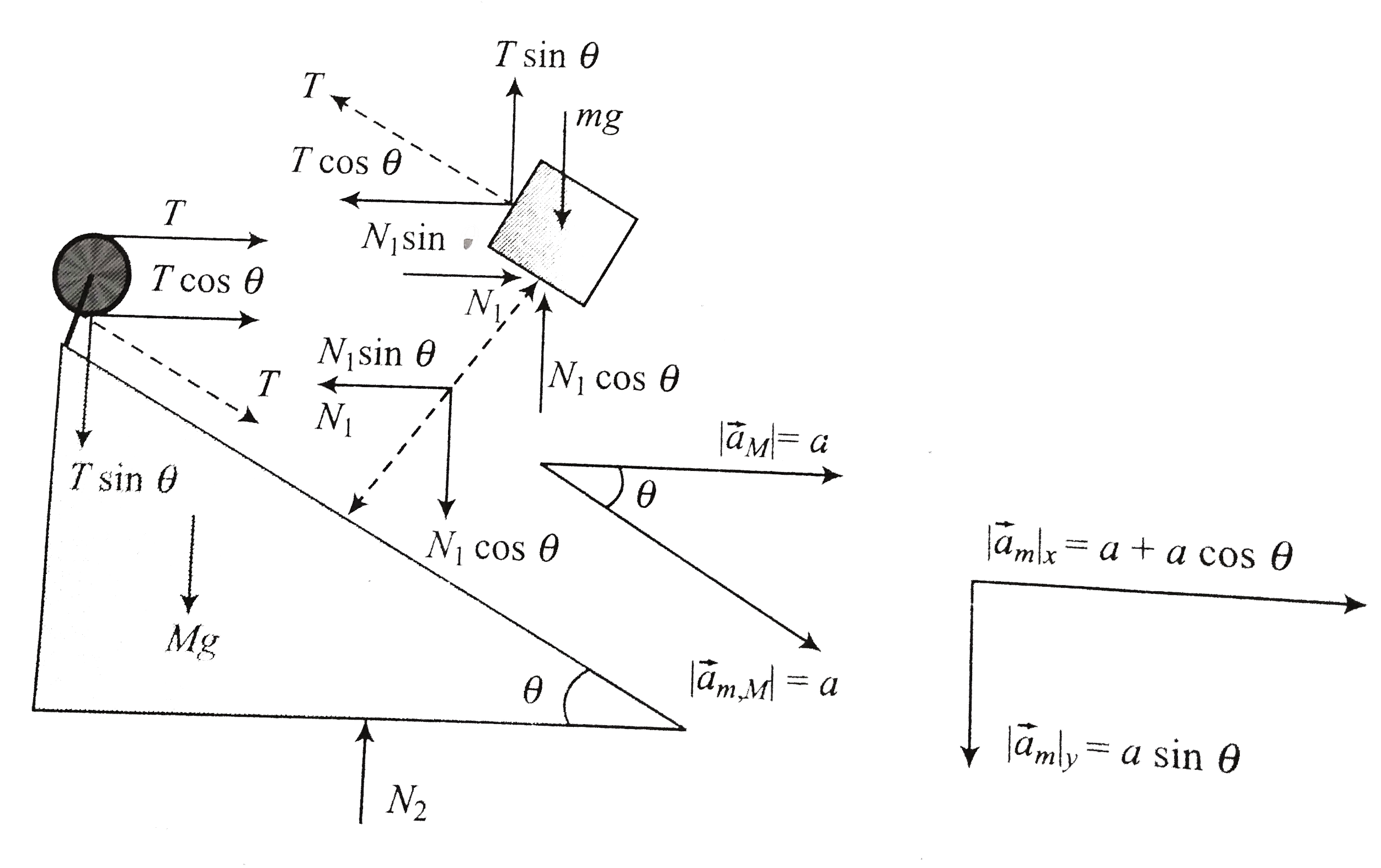
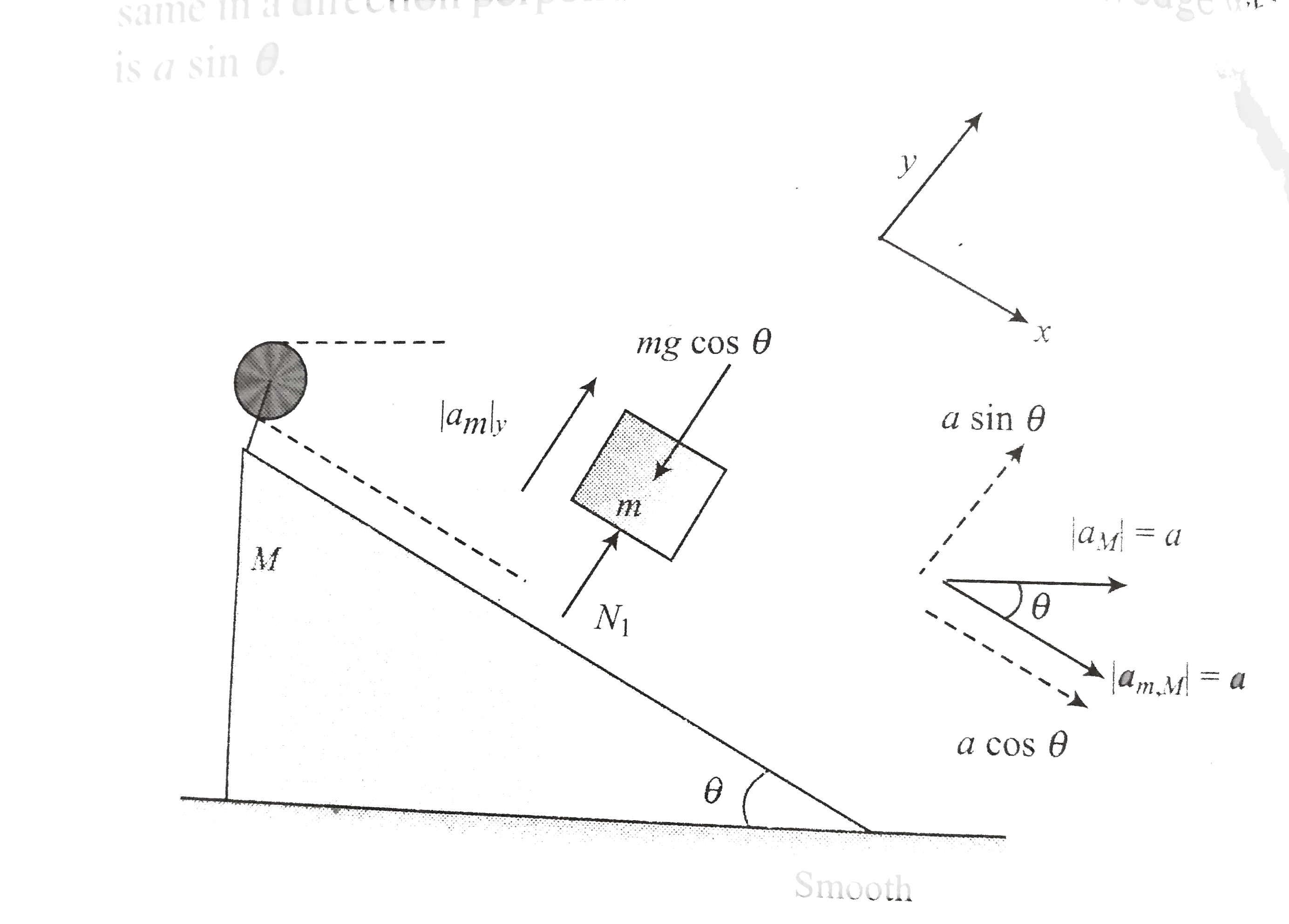
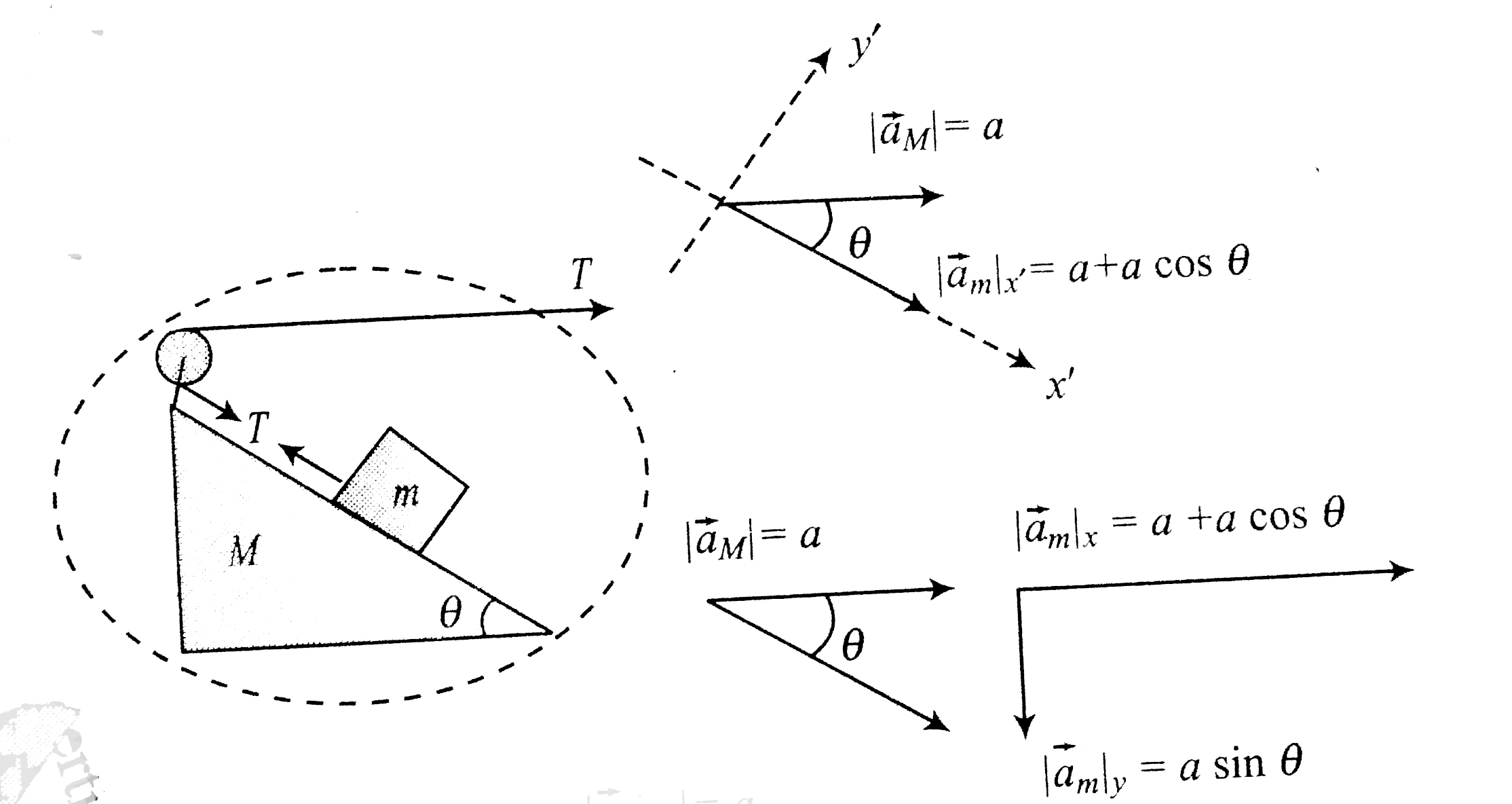
- In fig. mass m is being pulled on the incline of a wedge of mass M. Al...
Text Solution
|
- A block of mass m can slide freely in a slot made in a bigger of mass ...
Text Solution
|
- A block of mass m can slide freely along the verticle surface of a big...
Text Solution
|
- Consider a system of a small body of mass m kept on a large body of ma...
Text Solution
|
- In fig. mass m is being pulled on the incline of a wedge of mass M. Al...
Text Solution
|
- Three blocks arranged with pullwy and spring as shown in fig. If the s...
Text Solution
|