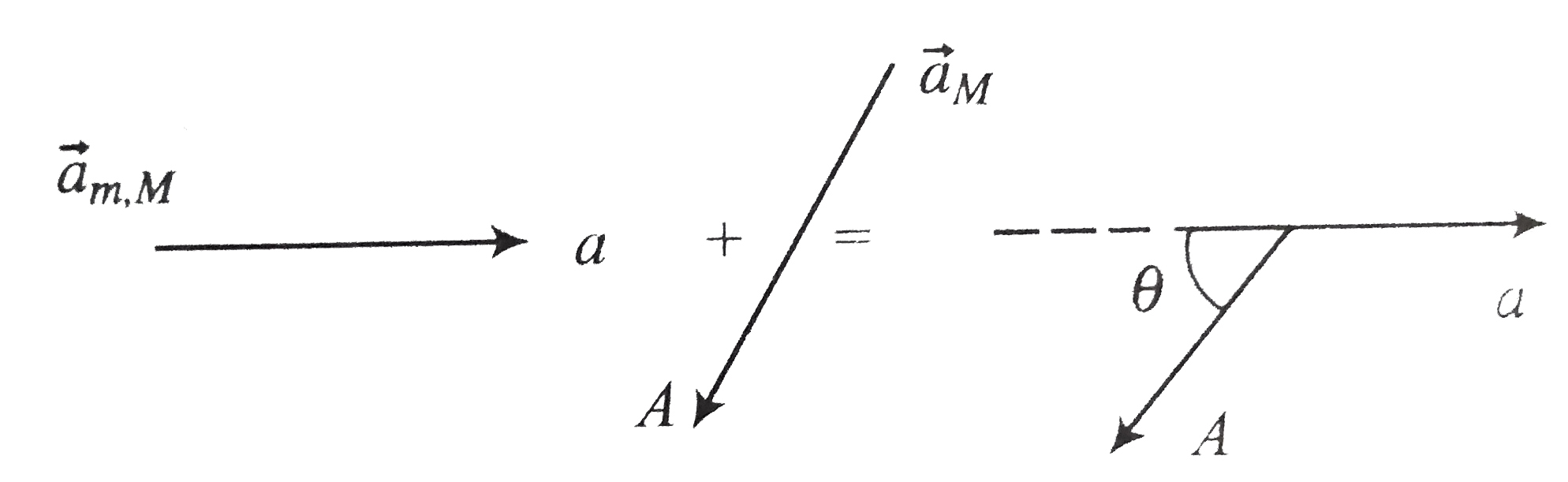Method 1: Analysis in an inertial reference frame attached to the ground :
Let a be the acceleration m w.r.t. M directed horizontally towards right.
Let A be the acceleration of M w.r.t. the ground directed along the incline downwards.

Acceleration of m w.r.t. ground will be the vector sum of the acceleration of m w.r.t. M and the acceleration of M w.r.t. ground.
force equation for m are
`0=m(a-A cos theta)` ..(i)
`mg-N'=m(A sin theta)` ...(ii)
Force equation for M are
`N' sin theta + Mg sin theta = MA` ...(iii)
`N' cos theta+Mg cos theta-N=0` ...(iv)
from (ii),
`N'=mg-mA sin theta`
Subsitituting `N'` in (iii),
`(mg-mA sin theta) sin theta+Mg sin theta =MA`
`implies A=((M+m)g sin theta)/(M+m sin^(2)theta)`
Acceleration of m w.r.t. ground is `A sin theta` (since, `A cos theta-a=0`). Thus, the acceleration of m w.r.t. ground is
`a_(mG)=A sin theta=((M+m)g sin theta)/(M+m sin^(2)theta)`
Method 2: Analysis of motion of m in the non-inertial reference frame attached to M:
Let the acceleration of M w.r.t ground be A along the inclined plane downwards. Consider that ground is an inertiail reference frame, the reference frame attached to M will be non-inertial . For applying Newton's second law of motion to any object w.r.t. on the object which equals mass of the objects times accelerations of M, directed opposite to A.
Force equation for m:
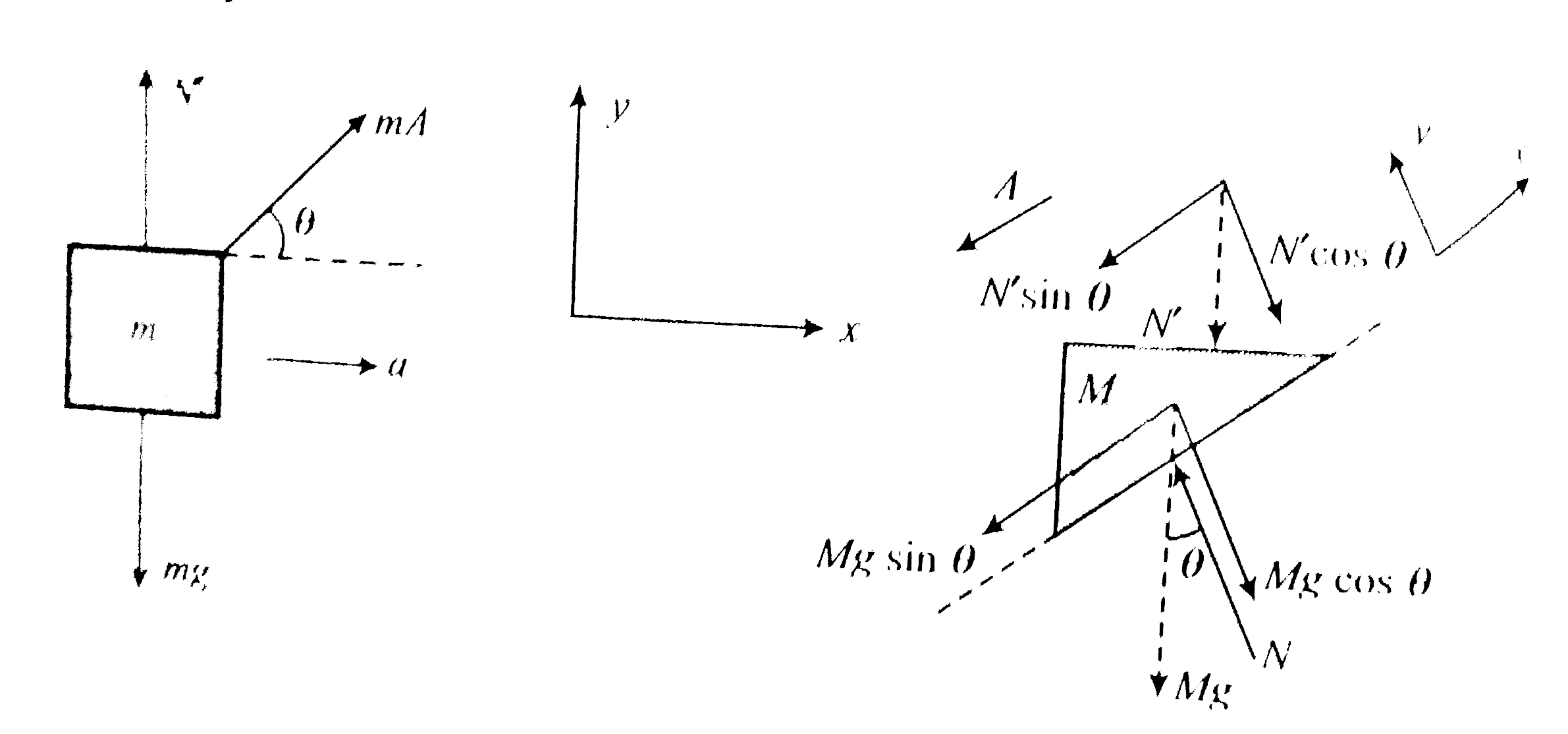
Let the acceleration of m w.r.t. M be a, in the horizontal direction towards right.
The force acting on m are:
`**`weight of m, mg, acting vertically downwards
`**` Normal force on m by M, `N'` , vertically upwards, and
`**` (mA), the inertial force acting along the incline upwards, as the acceleration of M is A along the incline downwards.
`N'+(mA) sin theta=mg` ..(i)
`(mA) cos theta=ma` ..(ii)
Force equation for M:
The force acting on M are
`**` The weight `Mg`
`** N'`, normal force exerted by m
`** N`, normal force exerted by the incline
`Mg sin theta+N' sin theta=MA`..(iii)
(Along the incline)
`Mg cos theta+N' cos theta =N` ...(iv)
(Perpendicular to the incline)
From (i),(iii) and (iv)
`A=((M+m)g sin theta)/(M+m sin^(2)theta)`
Acceleration of m relative to ground.
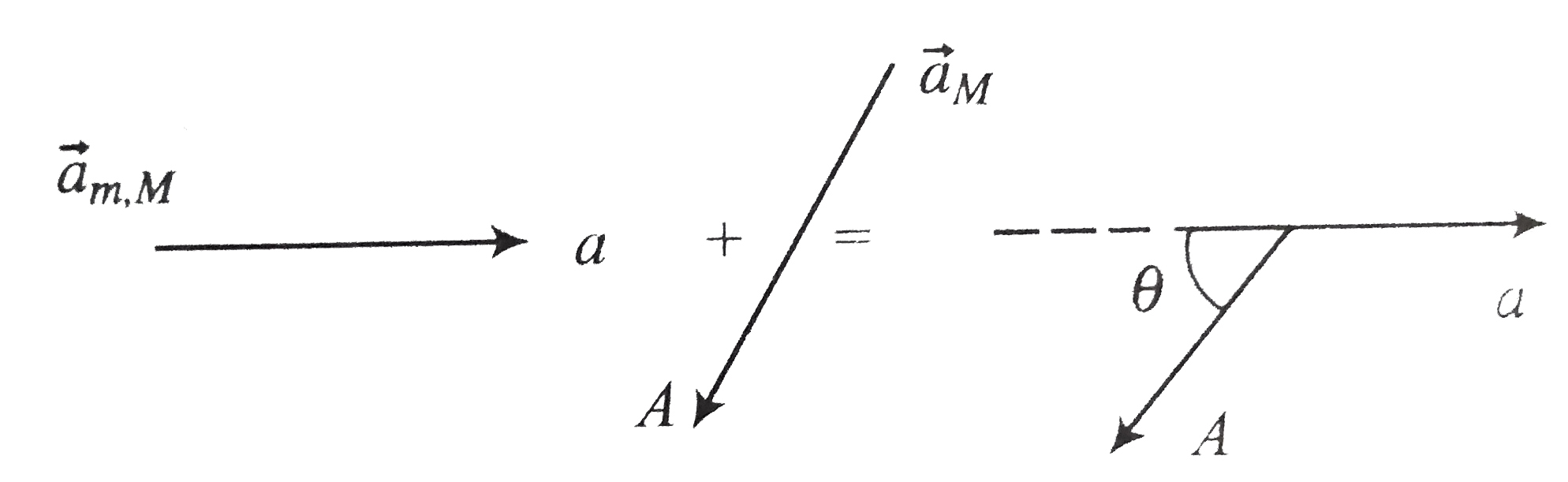
`vec(a)_(m)=vec(a)_(mM)+vec(a)_(M)`
`=ahat(i)+A cos theta (-hat(i))+A sin theta (-hat(j))`
But `a=A cos theta` [ form(ii)], therefore,
`a_(m)=A sin theta`, vertically downward
`((M+m)g sin^(2) theta)/(M+m sin^(2)theta)`
Method 3: Considering M and m as system

The system has `(M+m)g sin theta` external force parallel to inclined plane.
`vec(F)_(x')=M(vec(a)_(M))_(x')+m(vec(a)_(m))_(x')`
`(vec(a)_(m))_(x') = (vec(a)_(m,M))_(x') + (vec(a)_(M))_(x')`
`=-a cos theta + A =(A-a cos theta)`
`MA+m(A-a cos theta)=(M+m)g sin theta` ...(i)
Considering the motion of block in horizontal direction only and writing equation of motion w.r.t. ground,
`(vec(a)_(m))_(x)=a- A cos theta`
The block is not having any external force in horizontal direction
`Sigma vec(F)_(x) = 0 =m(vec(a)_(m))_(x)=m(a=A cos theta)`
or `a=A cos theta` ...(ii)
From (i) and (ii)
`MA+m[A-(A cos theta) cos theta]=(M+m)g sin theta`
`MA+mA sin^(2)theta=(M+m)g sin theta`
After solving, we get
`A=((M+m)g sin theta)/(M+m sin^(2)theta)`