Determine the magnitude of frictional force and acceleration of the block in each of the following cases :

Explanation

Case (i)`N_(1) = 100N , mg = 50N`
`f_(1) = mu_(s) N_(1) = 0.4 xx 100 = 40N`
`f_(k) = mu_(k) N_(1) = 0.3 xx 100 = 30N`

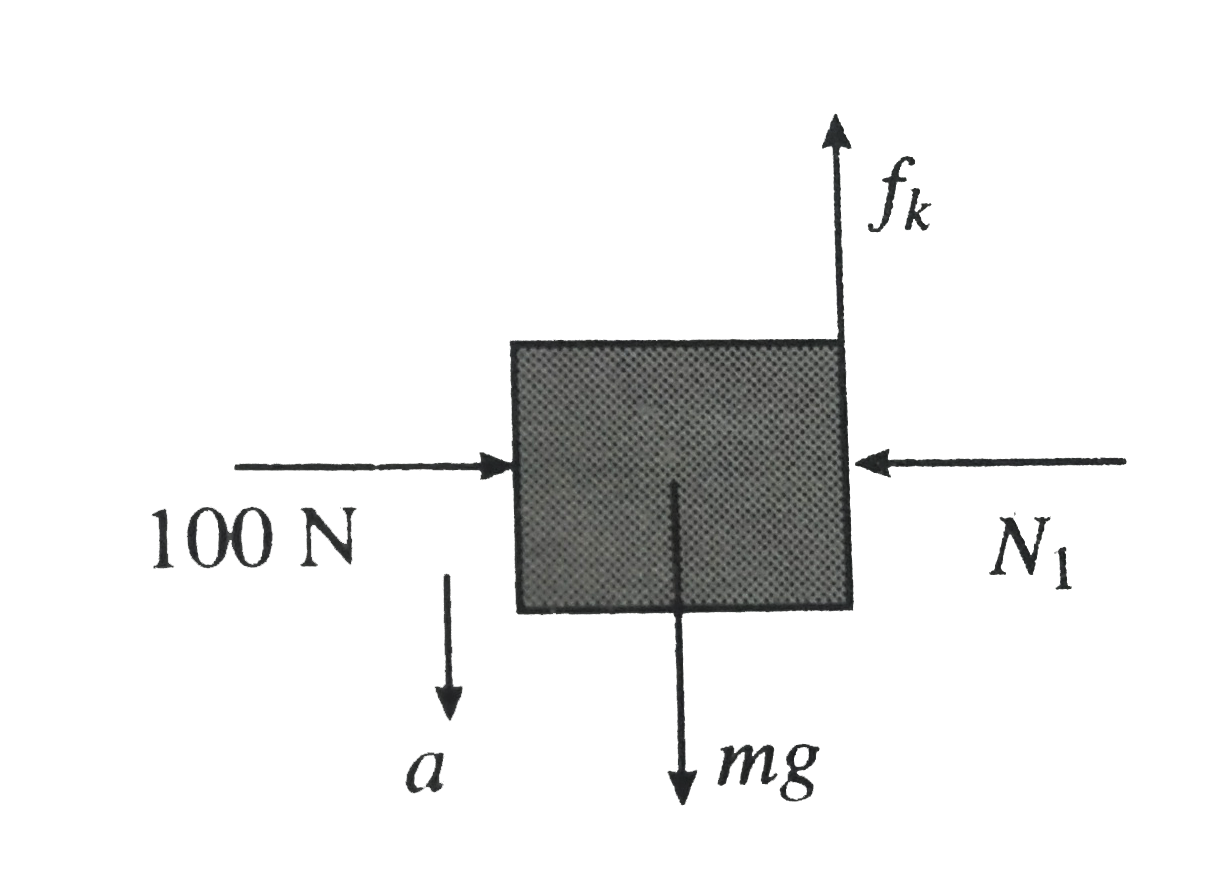
Here `mg` (driving force ) is greater than maximum friction `f_(1) = 40N` .Hence , the block will not be able to stay at rest if will accelerate downwards but where it starts slipping then kinetic friction will come into play. Now
`a = (mg - f_(k))/(m) = (50 - 30)/(5) = 4 ms^(-2)`
So, in this case ` f = f_(1) = 30N` and `a = 4 ms^(-2)` (downward)
Case(ii)
`N_(2) = 500N , mg = 50N`
`f_(1) = mu_(s)N_(2) = 200N`
`f_(k) = mu_(k) N_(2) = 150N`

Here `f_(1)` is graeter than `mg `(driving force) Hence block will not move so in this case `a = 0 , f= mg = 50N`
case III
`N_(3) = 400N`
`f_(1) = mu_(s)N_(3) = 160N`
`f_(k) = mu_(s) N_(3) = 120N`

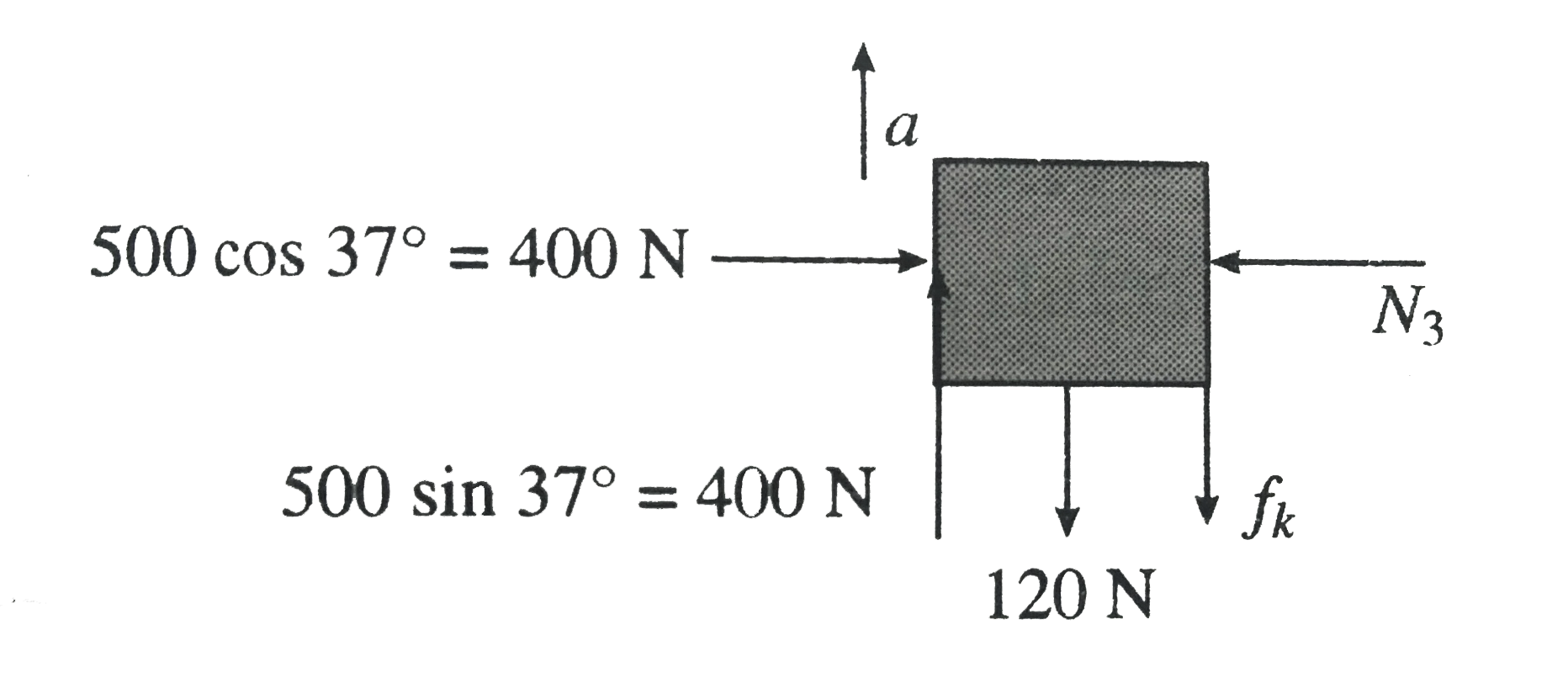
Here driving force `= 300 - 120 = 180 N` is apwards Driving force is more than `f_(1)` so the block will accelerate upward
`a = (180 - f_(1))/(m) = (180 - 120)/(12) = 5 ms^(-2) ` (upward)
So in this case,` f = f_(k) = 120N` and `5 ms^(-2)` (upwards)