Two blocks `A` and `B` are connected by a light inextensible string passing over a fixed smooth pulley as shown in figure The coefficient of friction between the block `A` and `B` the horizontal table is ` mu = 0.5 `. If the block `A` is just , find ratio of the masses of the blocks

Options

A. `(12)/(5)`
B. `(11)/(5)`
C. `(13)/(5)`
D. `(17)/(5)`

Answer

B

Explanation

From `FBD`of `A` and `B` shown in Fig the block `A` is just to slip . The friction will reach to it’s limiting value
`f_("lim")= mu N`….(i)

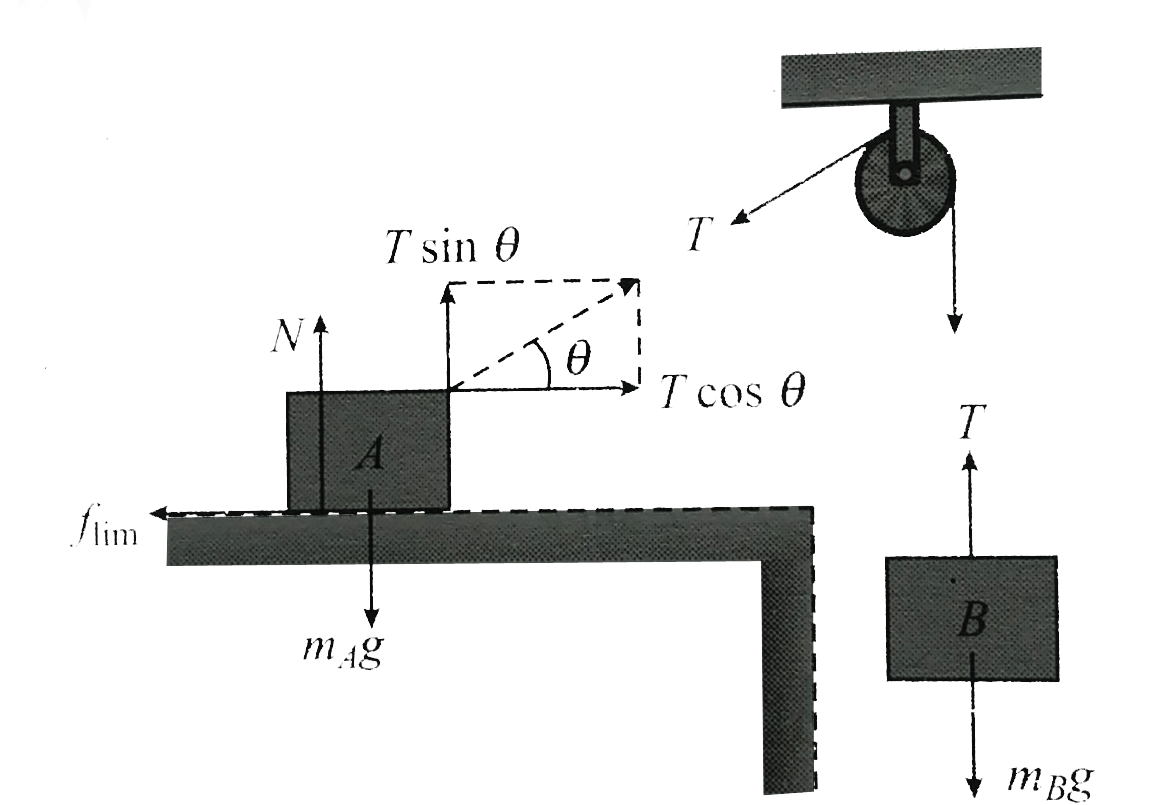
From `FBD` of `A`
`N + T sin theta = m_(0)A` ….(ii)
`T cos theta = f_(max)= muN`.....(iii)
From (ii), `N = m_(0)A - T sin theta `.....(iv)
From (iii) and (iv)
`T cos theta = mu m_(A)g - mu T sin theta` ....(v)
`T( cos theta + mu sin theta) = mu m_(0)A` ....(vi)
From `FBD` of `B,T = m_(B) g` ....(vii)
Taking ratio of (vi) and (vii)
`(mu)/(cos theta + mu sin theta)= (m_(B))/(m_(A))`
`:. (m_(A))/(m_(B)) = (cos theta + mu sin theta))/(mu) = (cos 37^(@) + (0.5)sin 37^(@))/((0.5)) = (11)/(5)`