The friction coefficient between the board and the floor shown in figure is `mu` Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

Explanation

Let `F `is the force applied by man on tope Hence tention in string ` T = F`
The man is equlibrium in verticle direction
Along verticle direction
`sum F_(v) , = 0` :
or `N + T = (M + m) g`

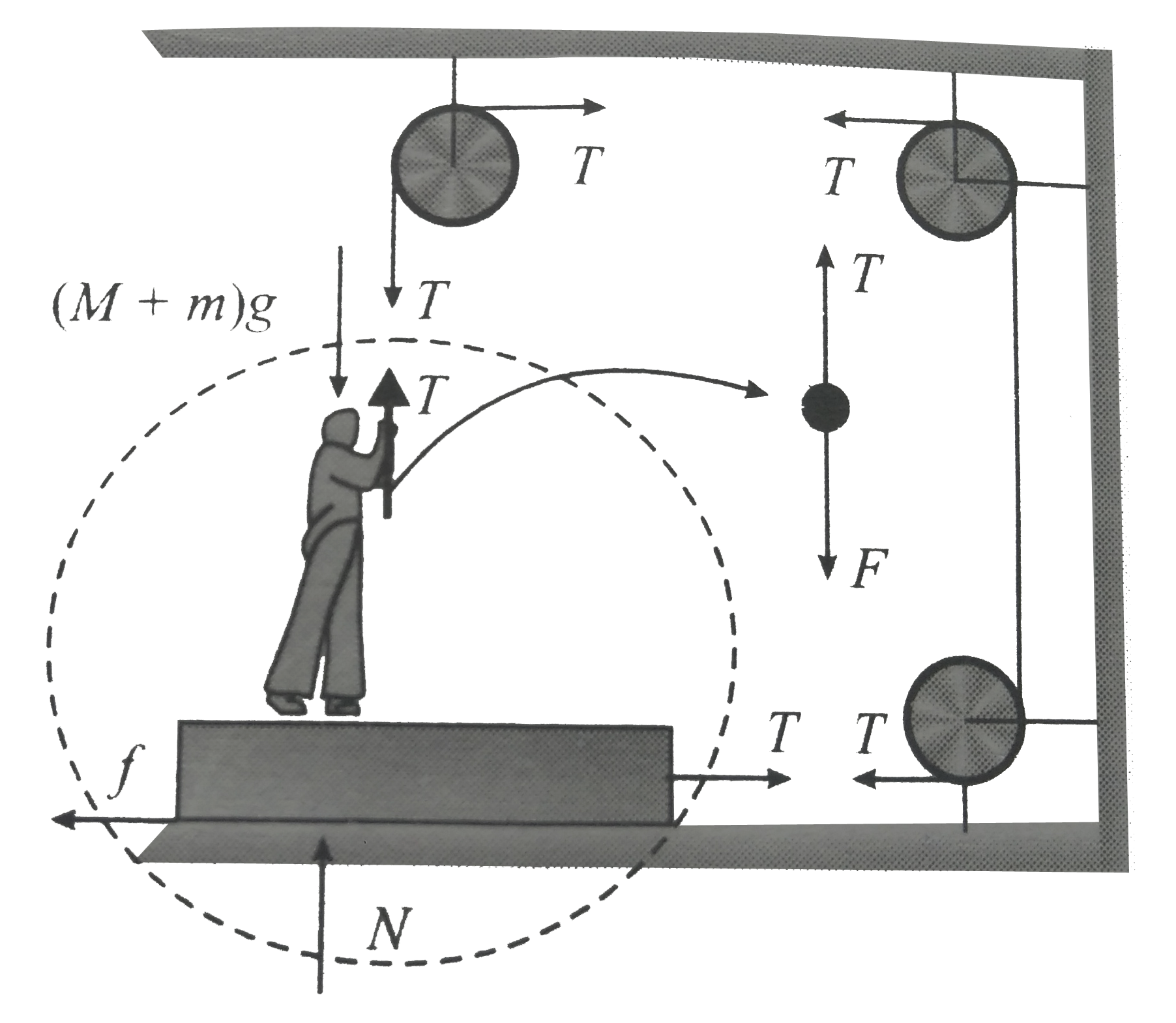
or `N = (M + m)g - T`
If horizontal direction of the beard is not sliding on floor then `f = T` and friction should static or `f le f_(max)`
The bread will not slip over the floor if `T le f`
For maximum value of `T` we have
`f = mu N = mu (M + m) g - T) = mu (M + m)g - mu T`
`rArr T = [(mu (M + m)g)/(1 + mu)]`
`But F = T Hence , F = [(mu (M + m)g)/(1 + mu)]`