A block of mass `m` lying on a horizontal surface (coefficient of static friction `= mu_(s))` is to be brought into motion by a pulling force `F` At what angle `theta ` with the horizontal should the force `F` be applied so that its magnitude is minimum ? Also find the minimum magnitude

Explanation

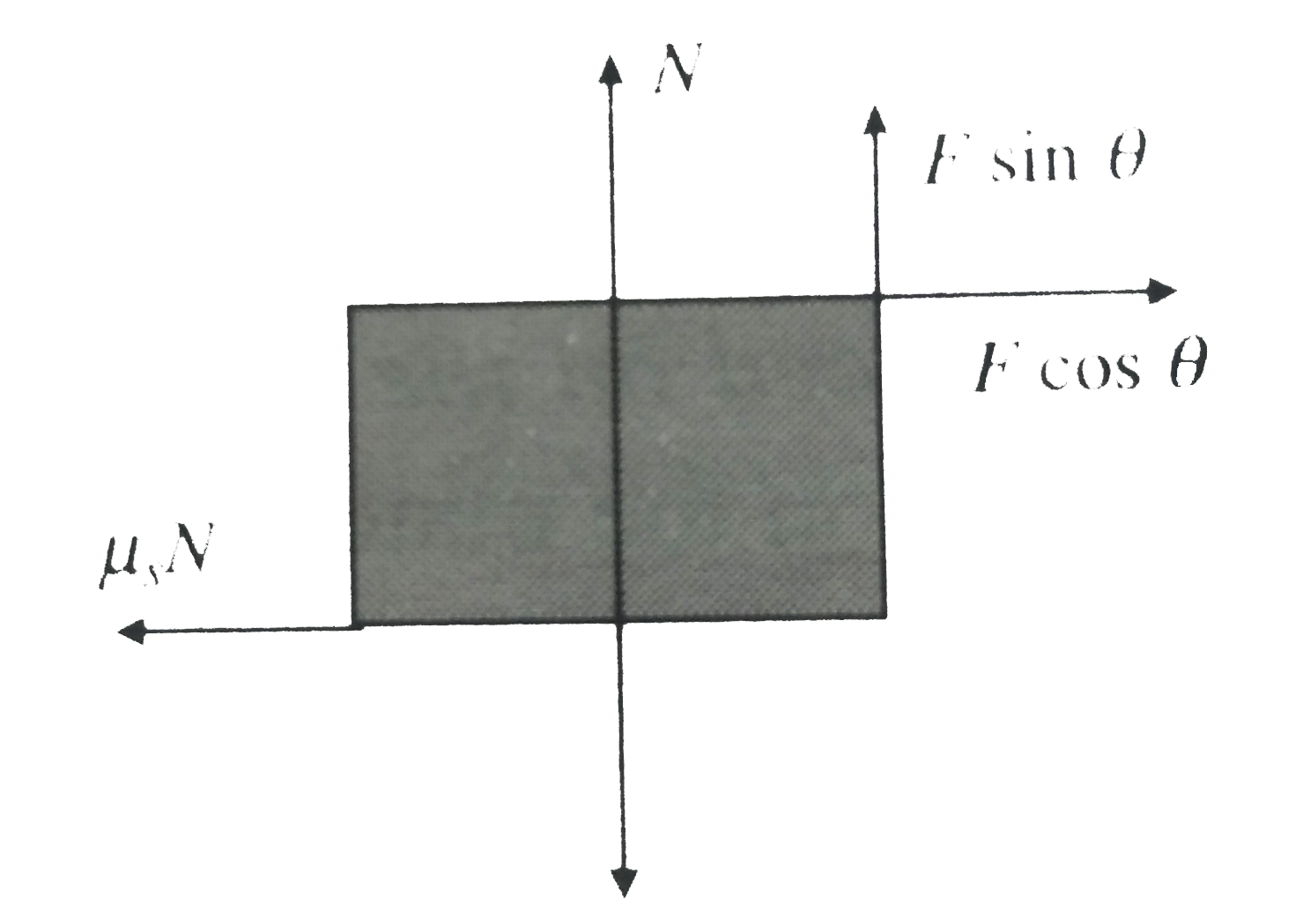
Let us first calculate the force `F` required to bring `m` into motion in terms of angle `theta ` Equation using laws of motion are as follows:
`N = mg - F sin theta`
and`F cos theta = mu_(0) N`
`F cos theta = mu, (mg - F sin theta )`
`rArr F = (mu_(s) mg)/(cos theta + mu_(s) sin theta) `
We have to find the angle `theta` For which this force `F` is minimum substituting `mu_(s) = tan theta ` (for simplification), we get
` F = (mg tan phi )/(cos theta + tan phi sin theta ) = (mg sin phi)/(cos (theta - phi ))`
`F` is minimum is `cos (theta - phi)`maximum ,Hence `F` is minimum for ` theta = phi = tan ^(-1) mu_(s)`, and `F_("min") = mg sin theta`
To bring `m` into motion with least effect force should be applied at an angular `tan ^(-1) mu_(s)` and should have a magnitude equal to
`F_("min") = mg sin phi = (mu_(s) mg)/(sqrt(1 + mu_(s)^(2))`