A `5 kg` block is projected upwards with an initial speed of `10 ms^(-1)` from the bottom of a plane inclined at `30^(@)` with horizontal . The coefficient of kinetic friction between the block and the plane is `0.2`
a. How far does the block move up the plane ?
b. How long does it move up the plate ?
c. After time from its projection does the block again come to the bottom ? What speed does it arrive?

Explanation

`5g sin 30^(@)` and `mu_(k)N ` both act downward , so acceleration a will be downward Therefore
`:. a = (5 g sin 30^(@) + mu_(e)N)/(5)`
`= g sin 30^(@) + mu_(k)g cos 30^(@)`
`= 6.7 ms^(-2) ( :' N = 5 g cos 30^(@))`
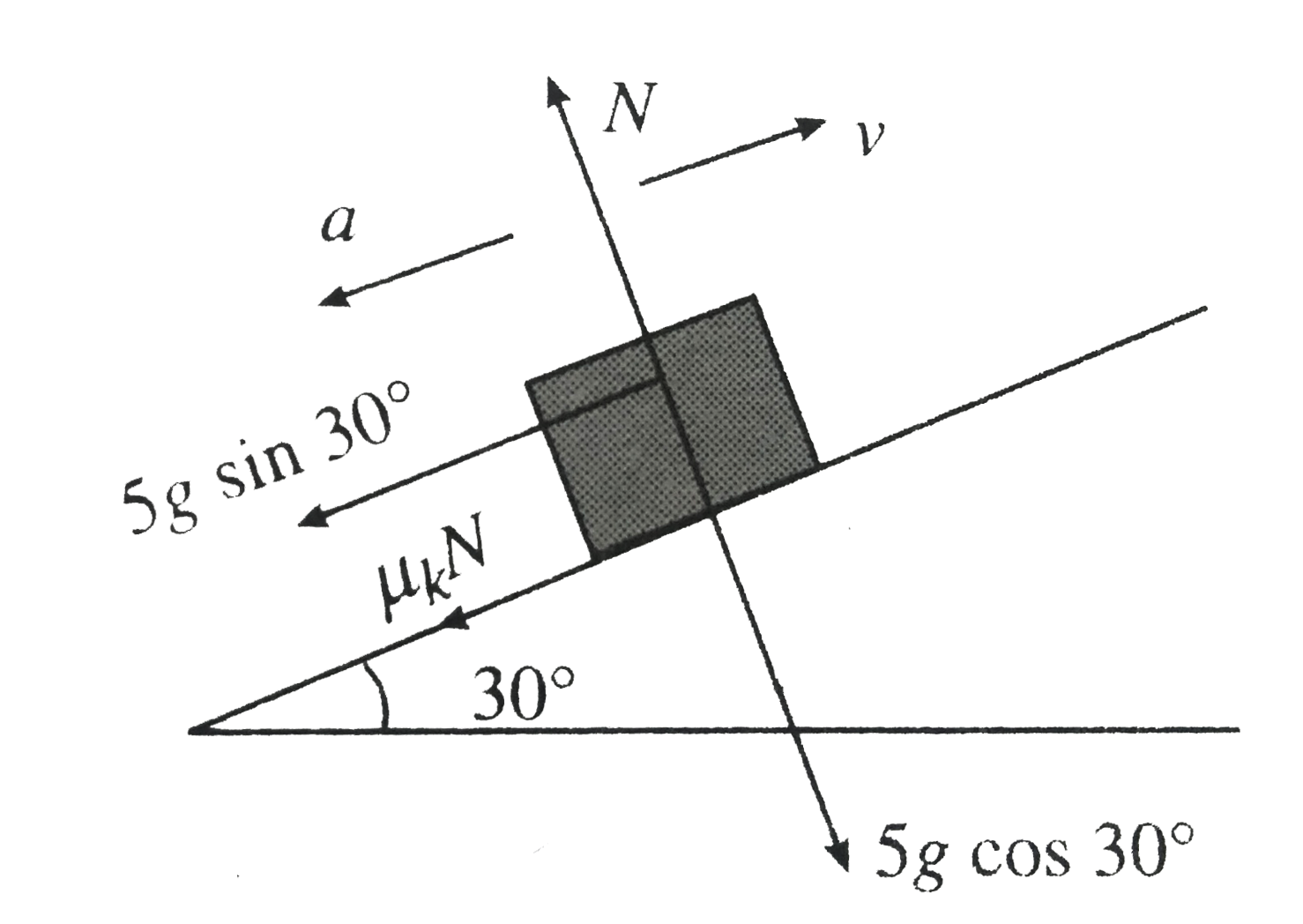
a. Find velocity is zero Let the block move up to distance `1` before stopping ` 0^(2) = u^(2) - 2 al`
`rArr l = (u^(2))/(2a) = (10^(2))/(2 xx 6.7) = 7.46 m `
b. ` v= u + at rArr 0 = 10 - 6.7 rArr r = 10//6.7 = 1.5 s`
c. In this case , friction will act in spward direction
` a = (5 g sin 30^(@) - mu_(s) N)/(5)`
`= 3.26 ms^(-2)`

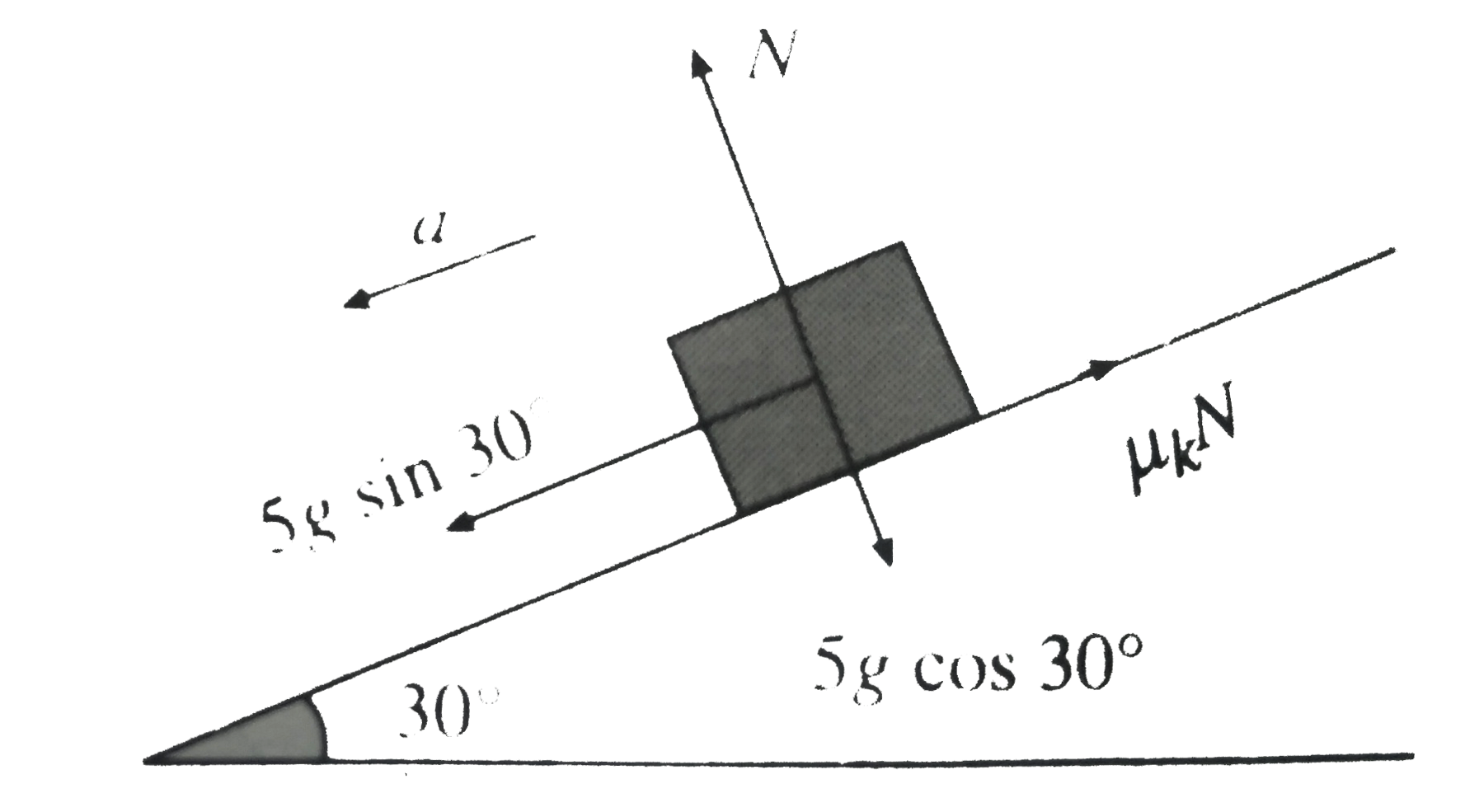
Let the time taken be `t` Block will start from rest
`l = (1)/(2) at^(2)rArr t = sqrt(2l la) = sqrt((2 xx 7.46)/(3.26)) = 2.14s`
Total time `= 1.5 + 2.14 = 3.64 s`