a. Here angle of repose `a = tan^(-1) (mu_(s))`
`alpha = Tan^(-1) ((1)/(2)) = 30^(@)`
The angle of inclination is greater than the angle of repose
For the acceleration of block .
`Mg sin theta - mu N= Ma`
`rArr a = g sin theta - mu g cos theta `
` = 10(sin 37^(@) - 0.5 cos 37^(@) )`
b. If external force `F = 75 N `is applied on the block
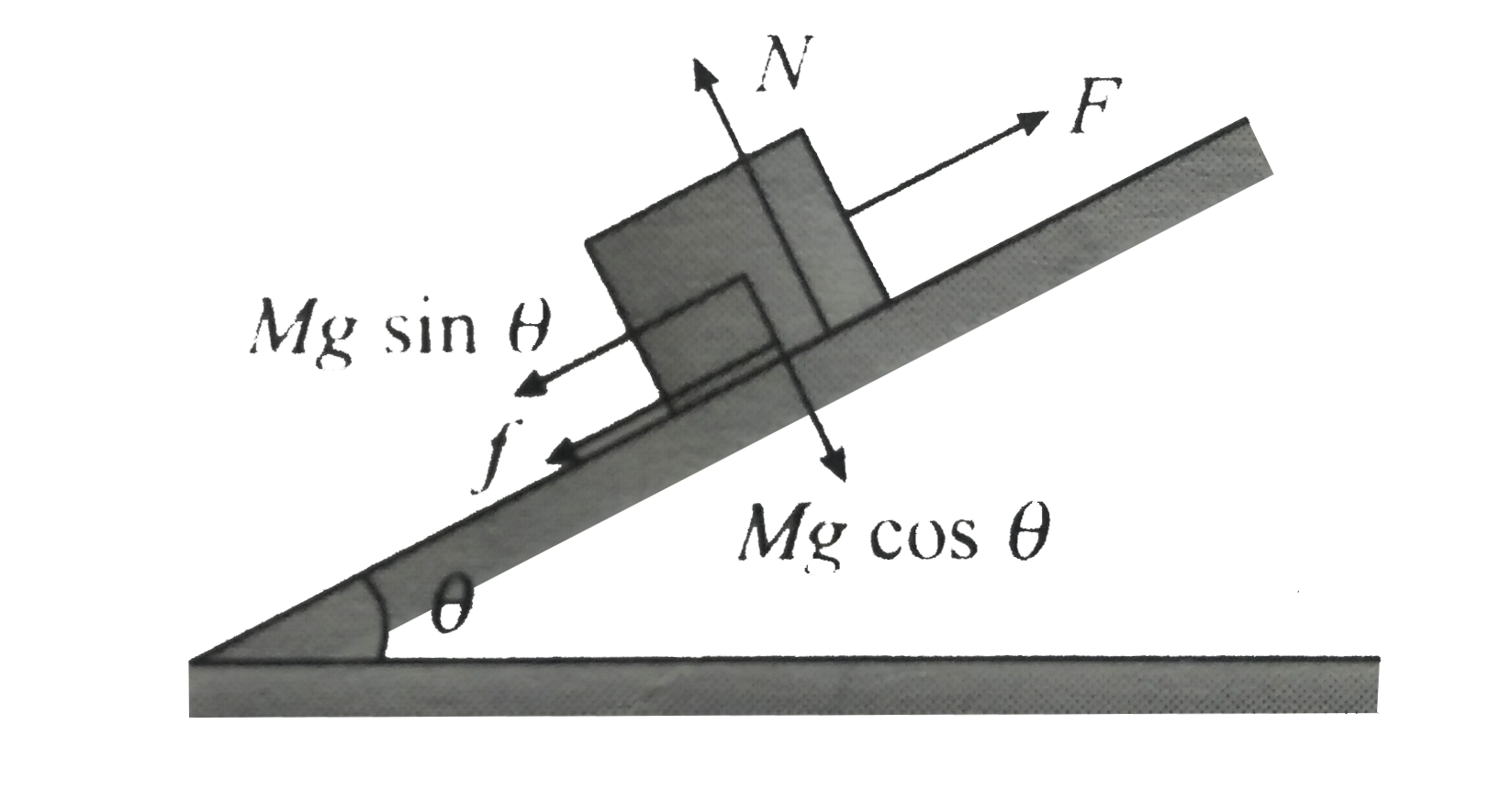
Let as find net driving force acting on block . parallel to incliend two externalforces are acting are one in upward direction `F` and other is the component of weight in the direction downward the plate `Mg sin theta `
Net driving force `f_("driving") = F - Mg sin theta`
`rArr F_("driving") = 75 - 10 xx 10 xx sin 37^(@) = 75 - 60 = 15 N`
Maximum resisting force that opposw relative motion maximum friction force (or `f_("lim"))`
` f_("lim") = mu_(s) Mg cos theta`
`= 0.5xx 10 xx 10 xx cos 37^(@) = 40N`
Here `F_("driving") lt F_("resisting")` Hence, the block will not move and friction will be static and will act is the direction opposite to driving force i,e in downward direction .
c. To move the block the least value of driving force should be `40HN`. But in above case, driving force is `15 N` (up)Hence if we add `deltaF = 25 N `in upward direction , the block will overcome maximum resistance force (or friction) as starts moving up
`:. 60 + 40 = 75 + delta F rArr deltaF = 25 N`
d. As resisting force which is maximum friction is `40N `and the component of weight parallel to incline is `60N` and acting downward If the only component of the weight in direction downward the incline plane
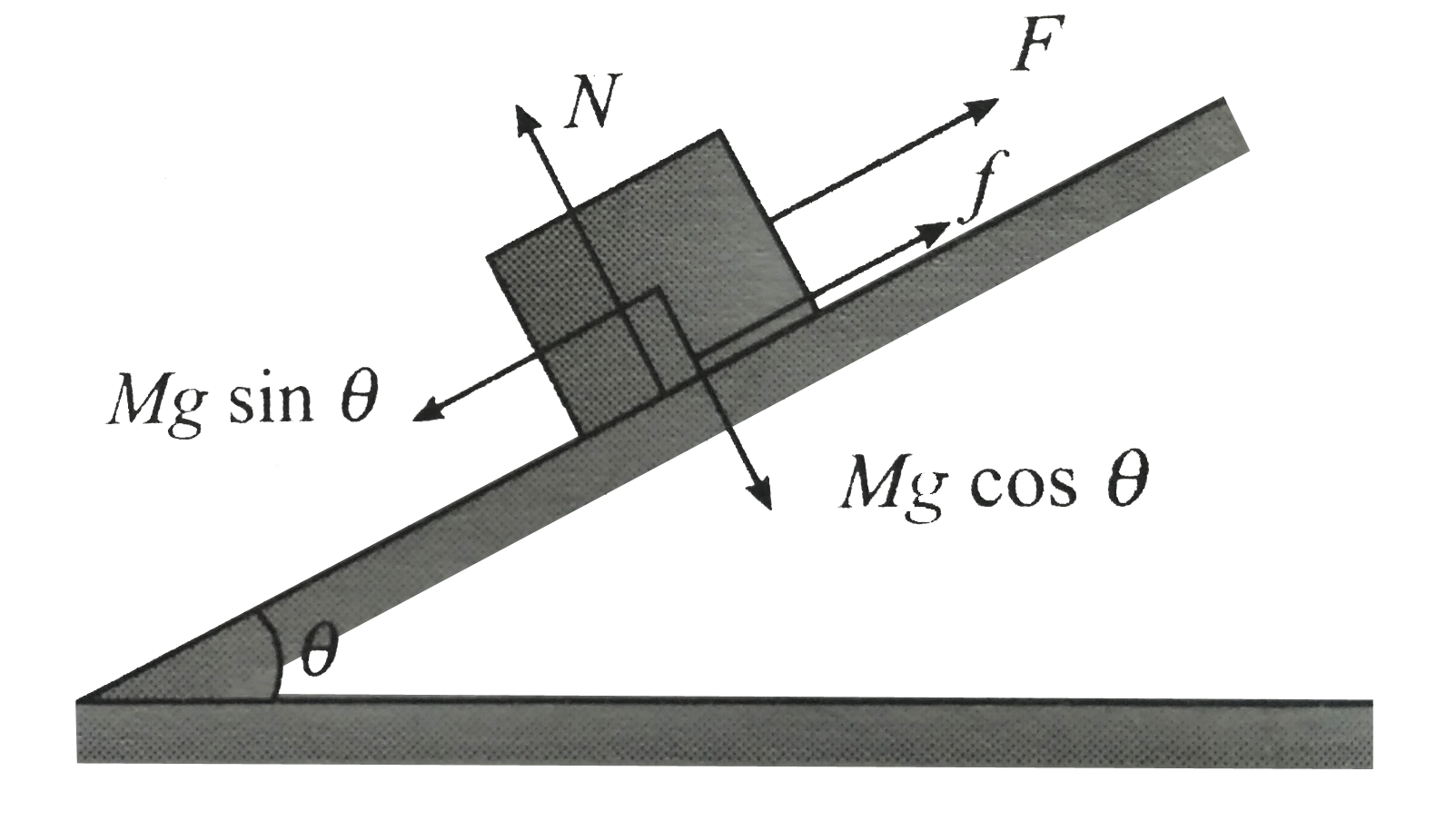
In this case , friction will act in upward direction hence the required value of `F` to make in equalibrium
`F + 40 = 60 `
or `F = 20N`