Block `A` of mass `m` and block `B` of mass `2m` are placed on a fixed triangular wedge by means of a light and inextensible string and a frictionless pulley as shown in fig . The wedge is inclined at `45^(@)` to the horizontal on both sides . The coefficient of friction between the block `A`and the wedge is `2//3` and that between the block `B` and the wedge is `1//3` .If the system of `A and B` is released from rest then find .
a. the acceleration of `A`
b. tension in the string
c.the magnitude and direction of the frictional force acting on `A`

Explanation

For finding the direction of friction first assume there is no friction any where in the absence of friction block `B` will move down the plane and the block `A` will move up the plane.Friction force oppose this motion

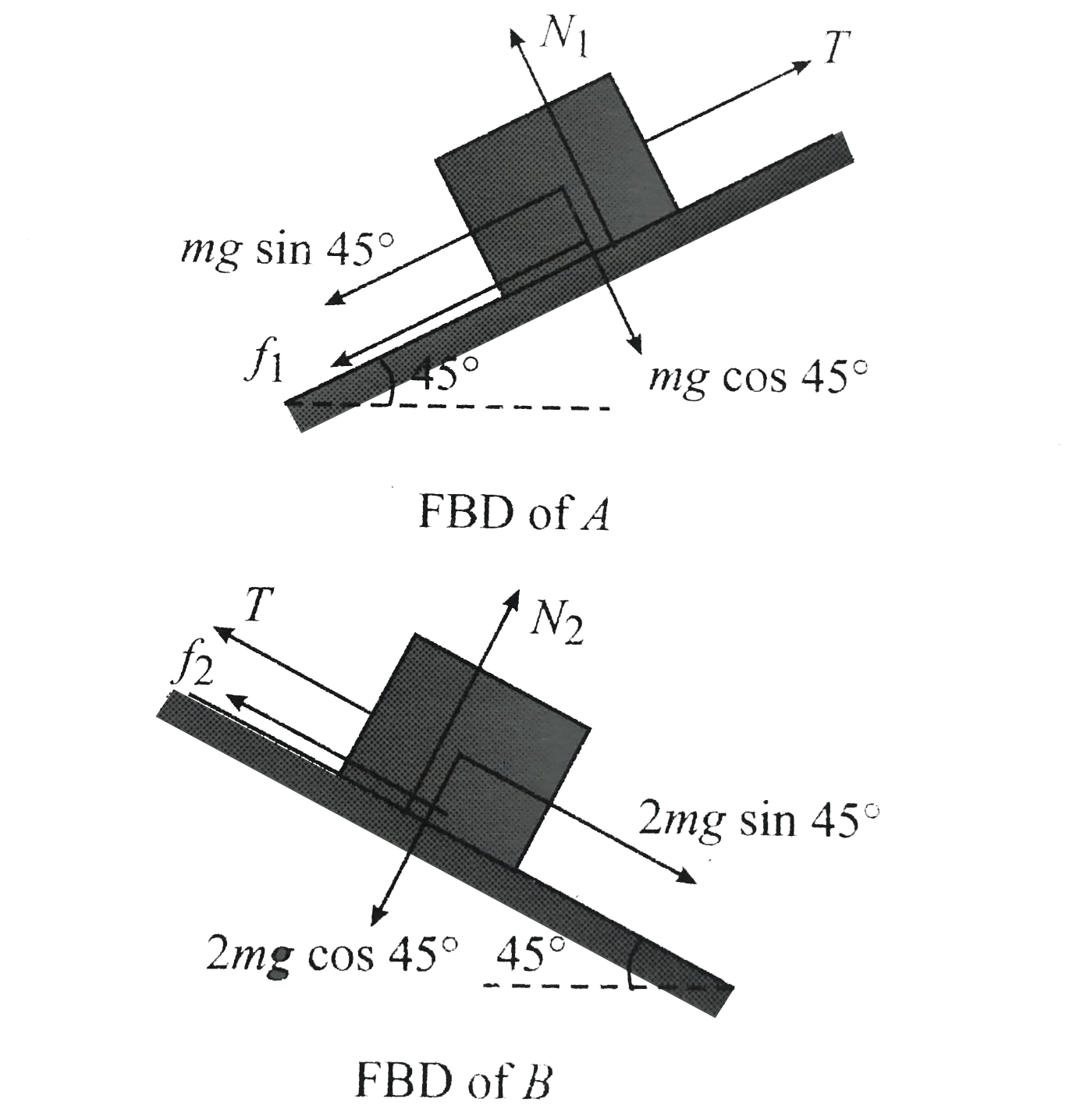
`FBD` of block `A`
`rArr T - mg sin 45^(@) - f_(1) = ma` ...(i) From `FBD` of `B`
`2mg sin 45^(@) - f_(2) - T = 2ma` ....(ii)
Adding (i) and (ii) we get
`mg sin 45^(@) - (f_(1) + f_(2)) = 3ma`
For a to be non zero `mg sin 45^(@)` must be greater than the maximum value of `(f_(1) + f_(2))` Therefore
`(f_(1) + f_(2))_(max) = mu_(1)N_(1) + mu_(2)N_(2)`
` = (mu_(1)m_(1)) + 2mu_(2)m_(2)g cos 45^(@)`
` = (4)/(3) mg cos 45^(@)`
`rArr mg sin 45^(@) lt (f_(1) + f_(2))_(max)`
Hence, block will remain stationary
b. `FBD` of block `B`
` mu_(2)N_(2) = (1)/(3) 2 mg cos 45^(@) = (2)/(3sqrt(2))mg `
Component of weight of `B` paralled to inclined plane
`(W_(||))_(B) = 2 mg sin 45^(@) = (2 mg)/(sqrt(2))`
Because `2 mg sin 45^(@) gt f_(2 (max))` ,therefore block `B` has the tendency to side down the plane
For block `B` to be at rest
` T + f_(2 (max)) = 2 mg cos 45^(@)`
`rArr T = (mg)/(sqrt(2)) (2 - (2)/(3)) = (4 mg)/(3sqrt(2)) = (2sqrt(2))/(3) mg`
c. Commponant of weight of `A` parallel to inclined plane
`(W_(||))_(A)= mg sin 45^(@) = (mg)/(sqrt(2))`
As `T gt (W_(||))_(A)` hence block `A` has the tendecy to move up the plate Therefore friction force on the block `A` will be down the plane
For `A` to be at rest
` FBD` at `A mg sin 45^(@) + f = T `
`rArr f = T - mg sin 45^(@)`
` = (2sqrt(2)mg)/(3) - (mg)/(sqrt(2)) = (mg)/(3sqrt(2))`