Two blocks `A` and `B` of mass `10 kg` and `20 kg` respectivelly, are arranged as shown in figure In the figure given a constant force `F_(0) = 120 N `act on block `A` and a force zero discoss the direction and nature of friction force and the acceleations of the block for different value of `F`

Explanation

If the above situation , we see that the maximum possible value of friction between the block is
`f_(max) = mu_(s)m_(A) g = 0.3 xx 10 xx 10 = 30N`
Case 1 : when `F = 0`
Considering that there is no slipping between the blocks the acceleration of system will be
` a = (120)/(20 + 10) = 4 ms^(-2)`
From `FBD` of `B f = m_(B) a = 20 xx 4 = 80N`
But `f_(max) = 30N`

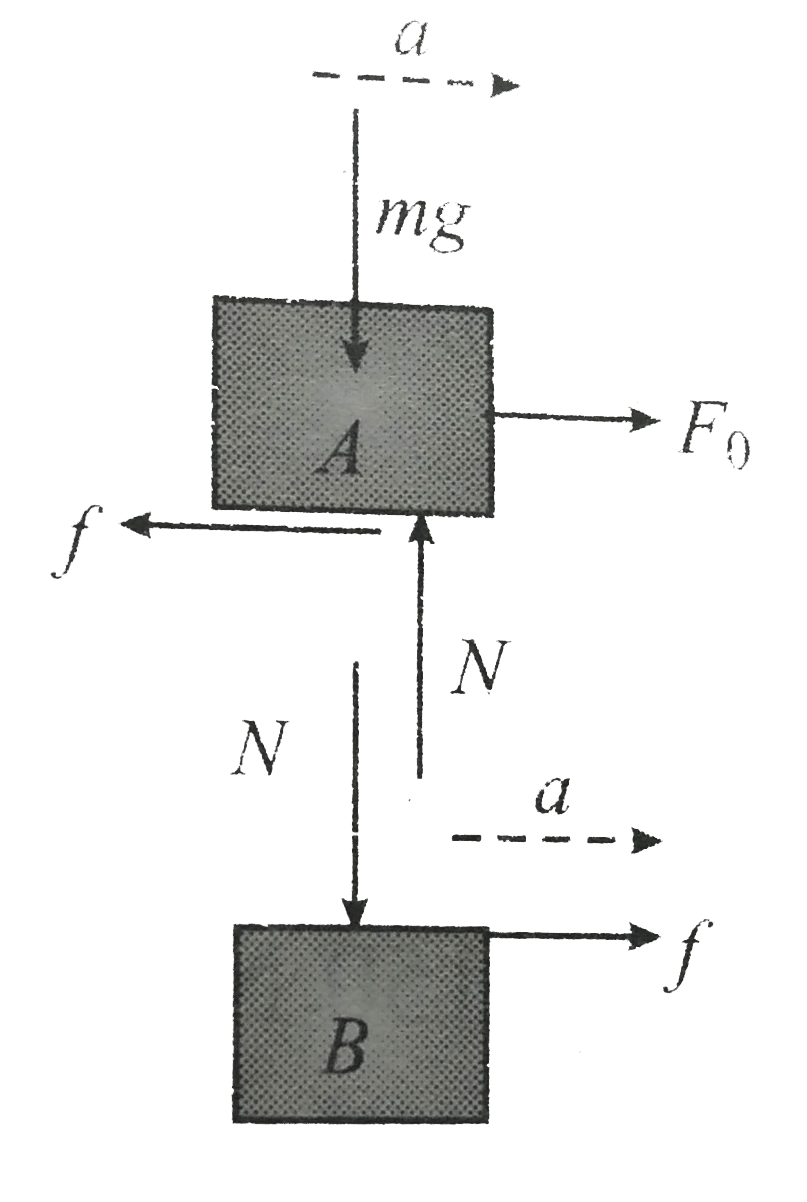
We can conclude that the blocks do not move togather.
New drawing the `FBD` of each , for finding out individual acceleration

Acceleration of `A`
`a_(A) = (120 - 30)/(10) = 9ms^(-2)` toward right
Acceleration of `B`
`a_(B) = (30)/(20) = 1.5ms^(-2)` toward right
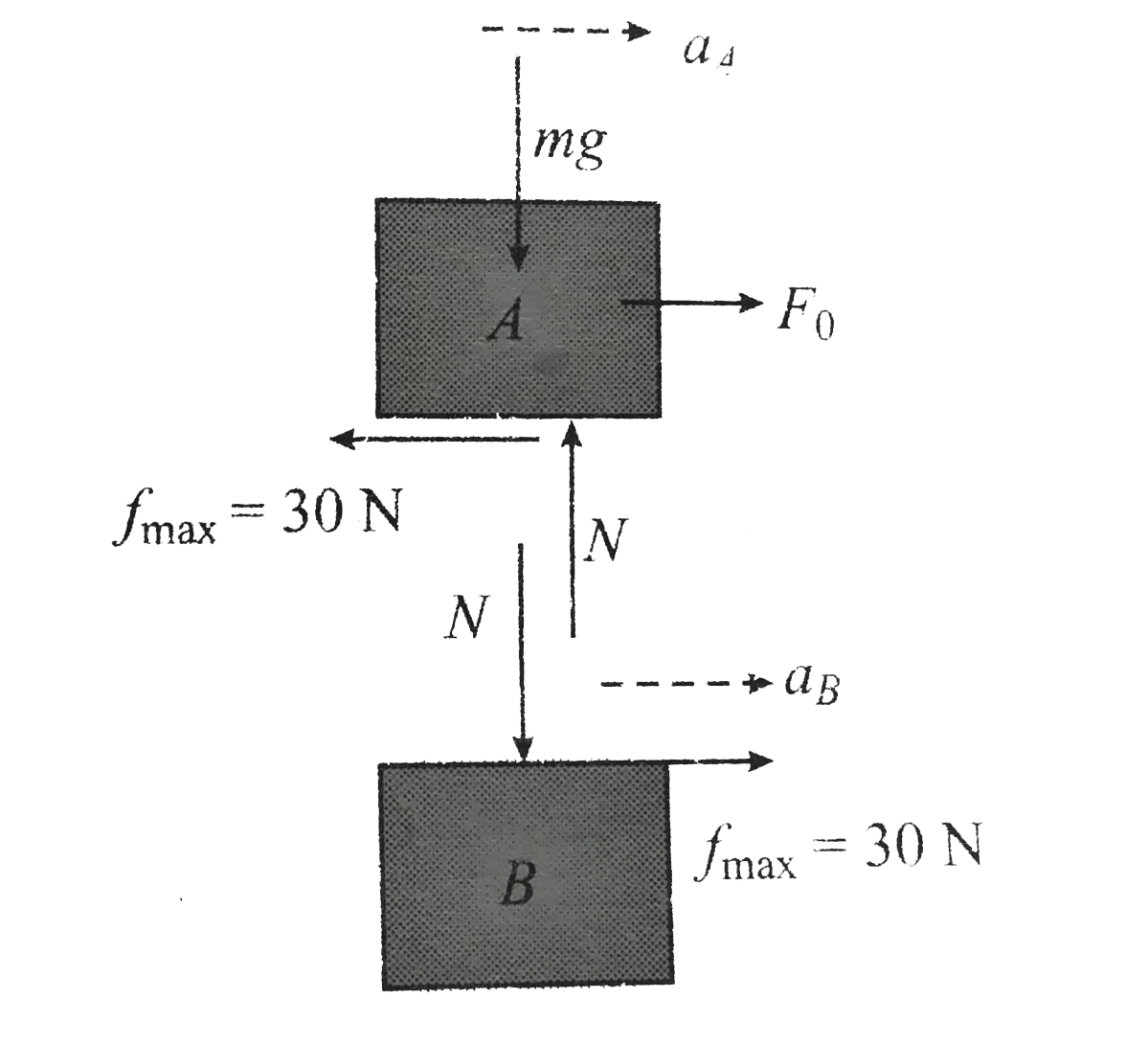
Case II: `F` is increased from zero till the two blocks just start moving togather .

As the two blocks move together , the friction is static in nature and its value is limiting `FBD` in this case will be
`a_(A) = (120 - 30)/(10) = 9ms^(-2)`
`rArr a_(B) = (F + 30)/(20) = a_(A) rArr (F + 30)/(20) = 9` or `F = 150N`
Hence , when `0lt F lt 150N` , the blocks do not move together and the friction is kinetic Asd `F` increase, acceleration of blocks `B` increases from `1.5ms^(-2) to 9 ms^(-2)`
At `F = 150N `, limiting static frictionstatic acting and the two blocks starts moving togather
Case III : When `F` is increased above `150N` In this scenario, the static friction adjusts itself so as to keep the blocks moving togather . The value of static friction starts reducing but the deriction still remain same This direction still the value of friction becomes zero In this case , the `FBD` is as follows

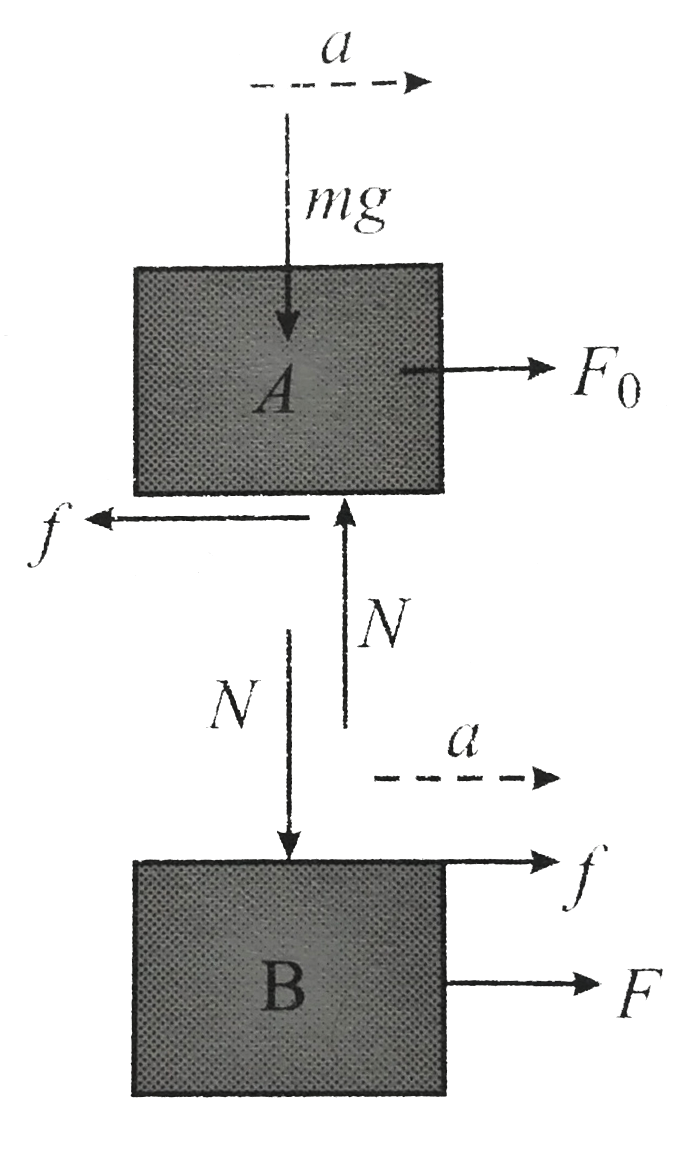
`a_(A) =a_(B) = (120 - f)/(10) = (F + f)/(20)`
Therefore when the friction force `f` gets reduced to zero , the above acceleration become
` a_(A)= (120 - 10)/(10) = 12ms^(-2) rArr a_(B)= (F)/(20) = a_(A) = 12ms^(-2) `
`:. F = 240 N`
Hence when `150N le F le 240N` the static friction force continously decreases from maximum to zero at `F = 240 N` , The acceleration of the blocks increases from `9 ms^(-2)` to `12 ms^(2)` during the change of force `F`
Case iv : when `F` is increased again from `240 N ` The decrease of friction firce on the block reveeses but it is still static `F` can be increased till this reverse static friction reaches its limiting value `FBD` at this jucture will be The blocks move togather , therefore

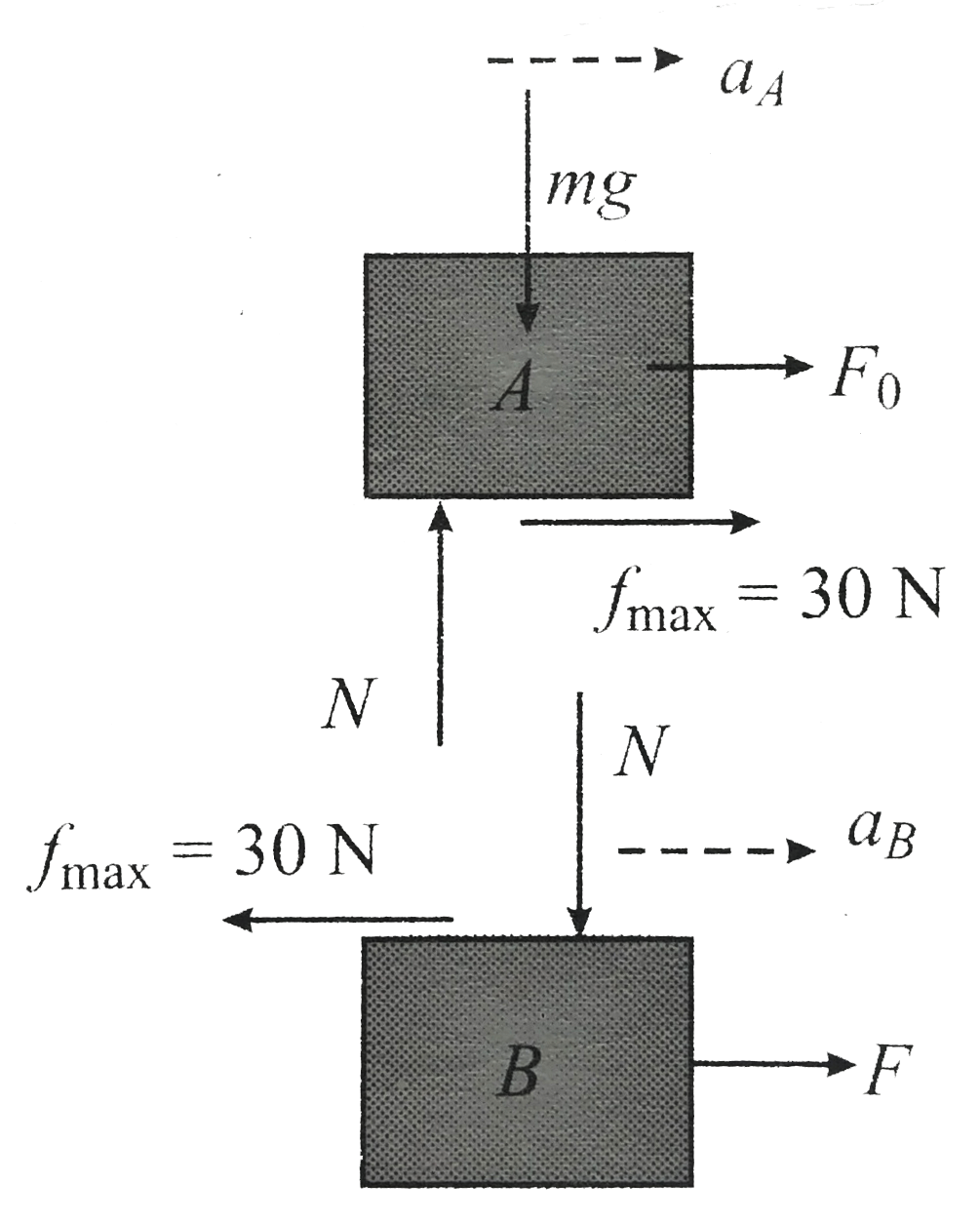
`a_(A) = (120 + 30)/(10) = 15ms^(-2)`
`rArr a_(B) = (F - 30)/(20) = a_(A) = 15ms^(-2)`
`:. (F - 30)/(20) = 15ms^(-2)`
Hence `F = 330 N`
Case V: When `F` is increased beyond `330 N` In this case . the limiting friction is achived and slipping takes place .