The masses of the blocks `A, B` and `C` shown in fig (a) are `4 kg, 2kg` and `2 kg` respectively Block `A` moves with an acceleration of `2.5 ms^(-2)`
a. Block `C` is removed from its in position and placed on block `A` (b). What is now the acceleration of block `C` ?
b. The position of the block `A` and `B` subsequently interchanged find the new acceleration of `C` .The coefficient of friction in the same for all the conect surface

Explanation

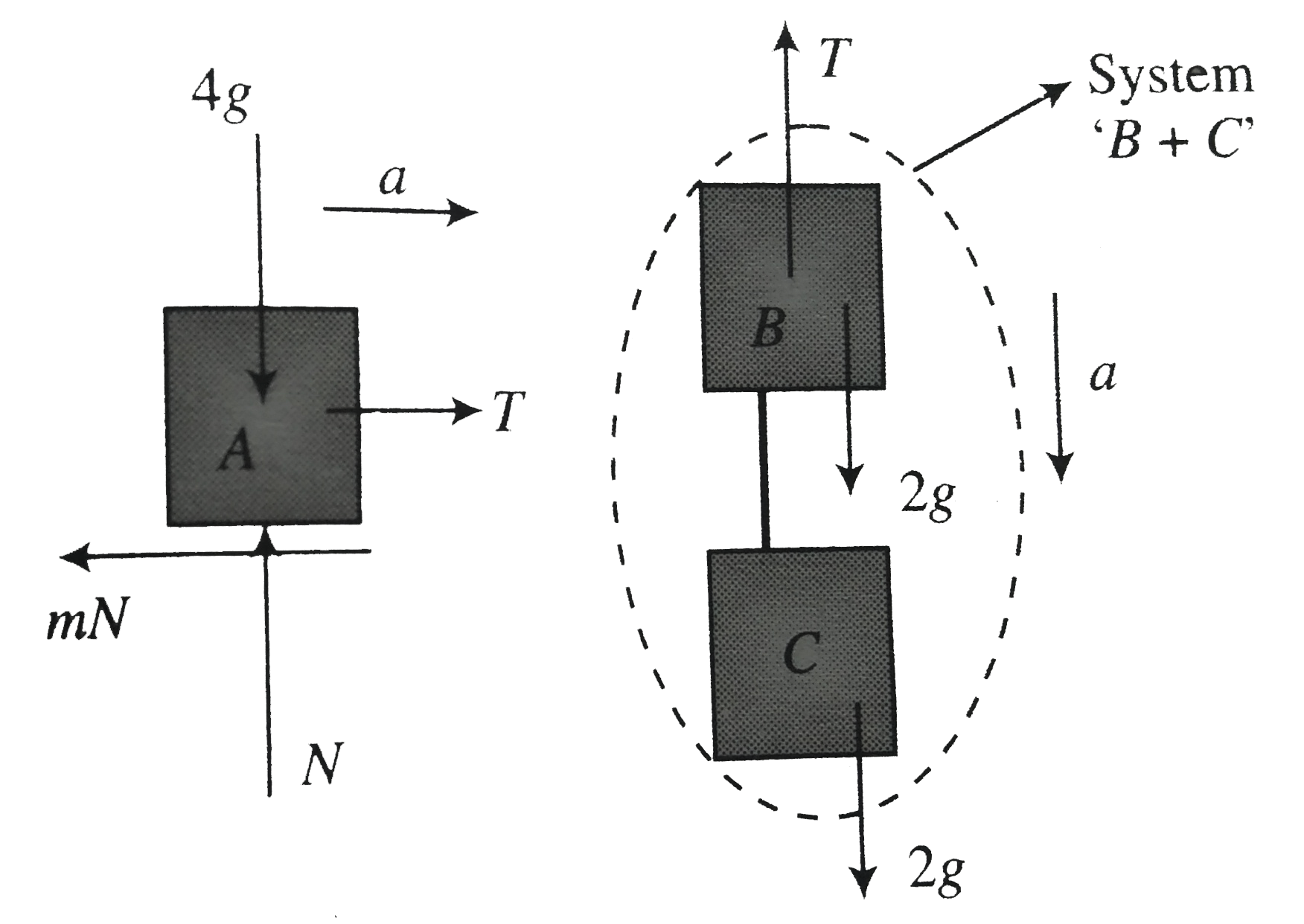
Given acceleration of the system , `a = 2.5ms^(-2)`
For `B` and `C : 2g + 2g - T = (2 + 2) g` ….(i)
For `A : T - mu N = 4a rArr T - mu 4 g = 4a` ....(ii)
Solving (i) and (ii) , we get `mu = 0.5`

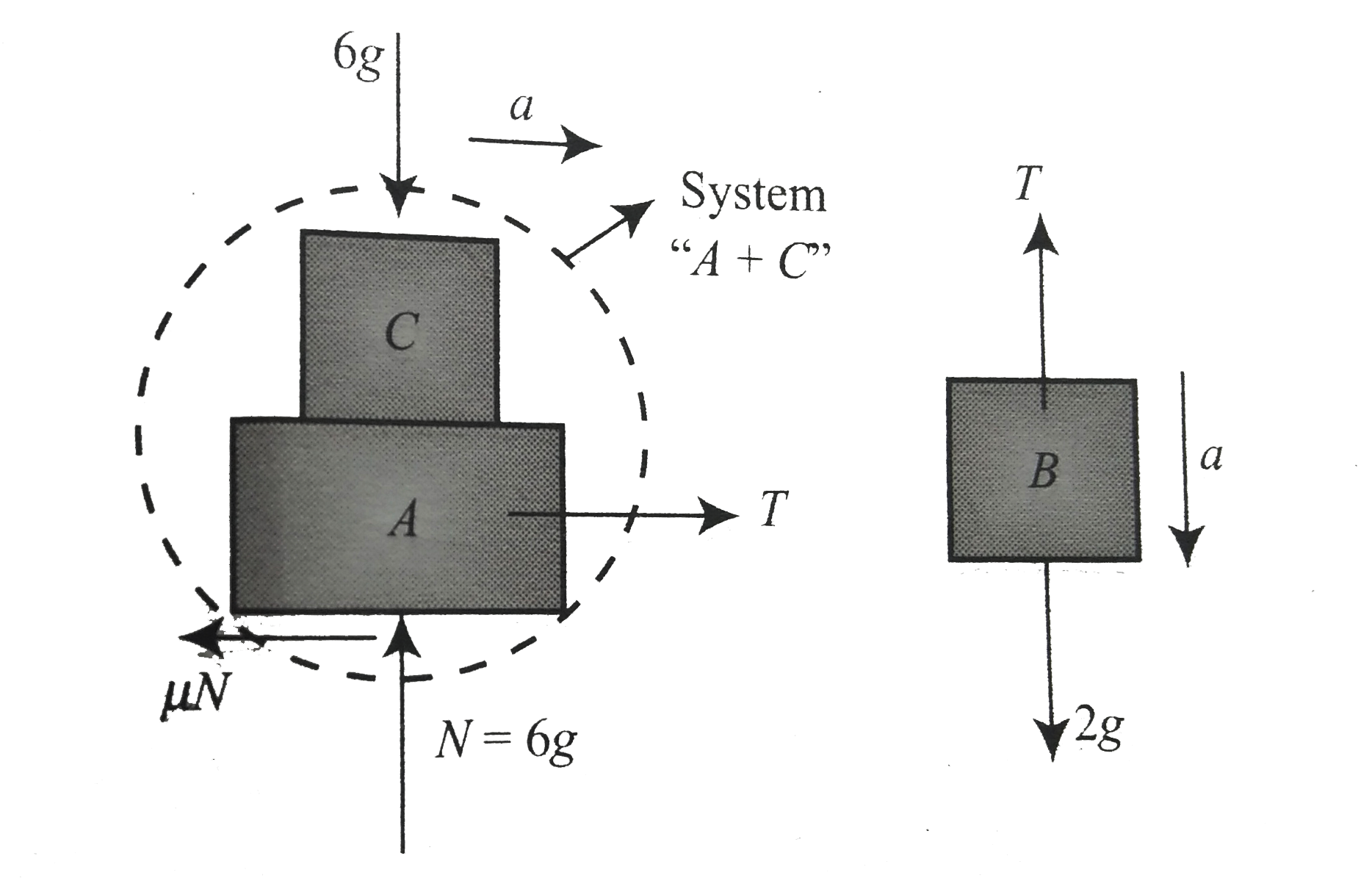
a. Let `A` and `C` move together with common acceleration `a` Then the acceleration of `B` is also a
` 2g - T = 2a` ....(i)
`T - mu 6 g = 6 a` ....(ii)
Solving these equation , a comes out to be negative , which is not possible, it means system will remain at rest and acceleration of `C` will be zero

b. Let `B` and `C` move together
`4g - T = 4a , T - 4mu g = 4a `
Solving them `a = 2.5 ms^(-2)`
Let `f` be the friction between `B` and `C` Then for `C`
`f = 2a = 2 xx 2.5 = 5N`
it is because this acceleration to `C` is given by friction `f` Limiting friction between `B` and `C f_(1) = mu 2g = (1//2) xx 2g = 10 N since f lt f_(1)` , so C will slip on `B` Hence , acceleration of `C = 2.5 ms^(-2)`