In the situation shown in fig
a. What minimum force `F` will make any part or whole system move?
b. Find the acceleration of two blocks and value of friction at the two surface if `F = 6 N`

Explanation

Between `4 kg` and ground :
`f_(t_(1)) = f_(k_(1)) = mu_(1) (2 + 4) g = 6 N`
Between `2 kg` and `4 kg:`
`f _(t_(2)) = f_(k_(2)) = mu_(2) g = 4 N`
a. Limiting friction between `2kg` and `4 kg` is less than that between `4kg` and ground. So `2kg` will slip over `4kg` if
`F gt f_(1_(2)) =4N rArr F_("min") =4N`
b. Let us consider the `FBD` of `4kg`: Acceleration to `4 kg` block will be provided by `f_(2)` But the maximum value of `f_(2)` is less than the maximum value of `f_(1)` Hence `4 kg` will not acceleration so `a_(0) = 0 `

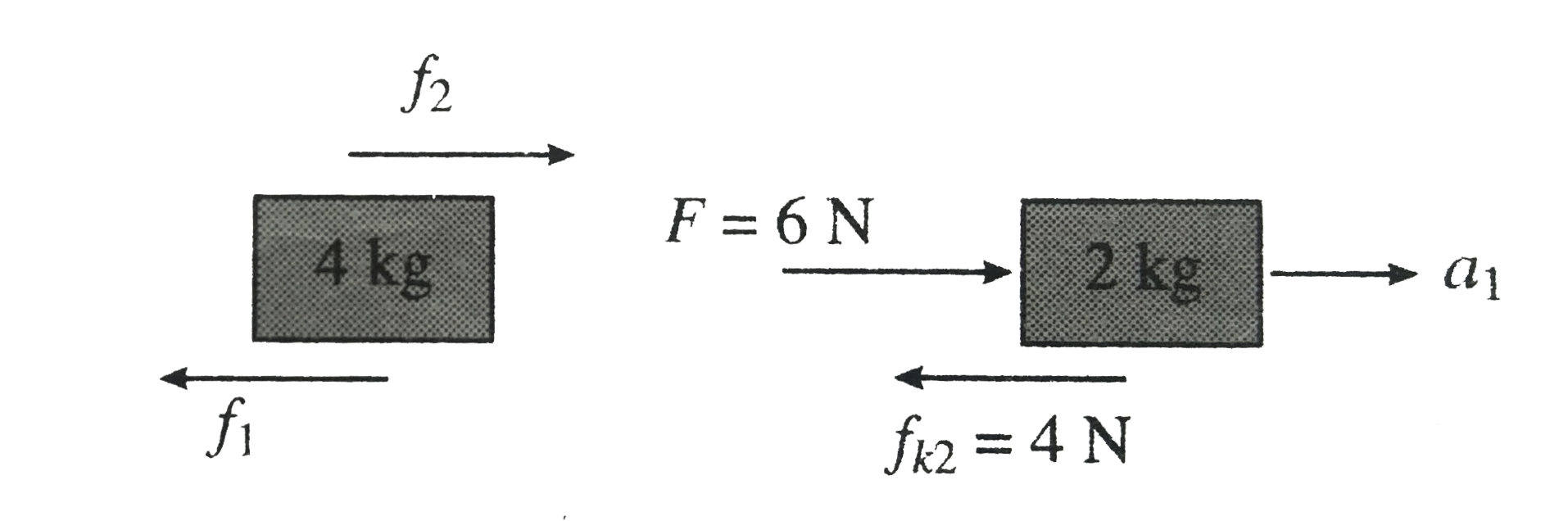
For `2 kg : a_(1) = (6 - 4)/(2) = 1 ms^(-2)`