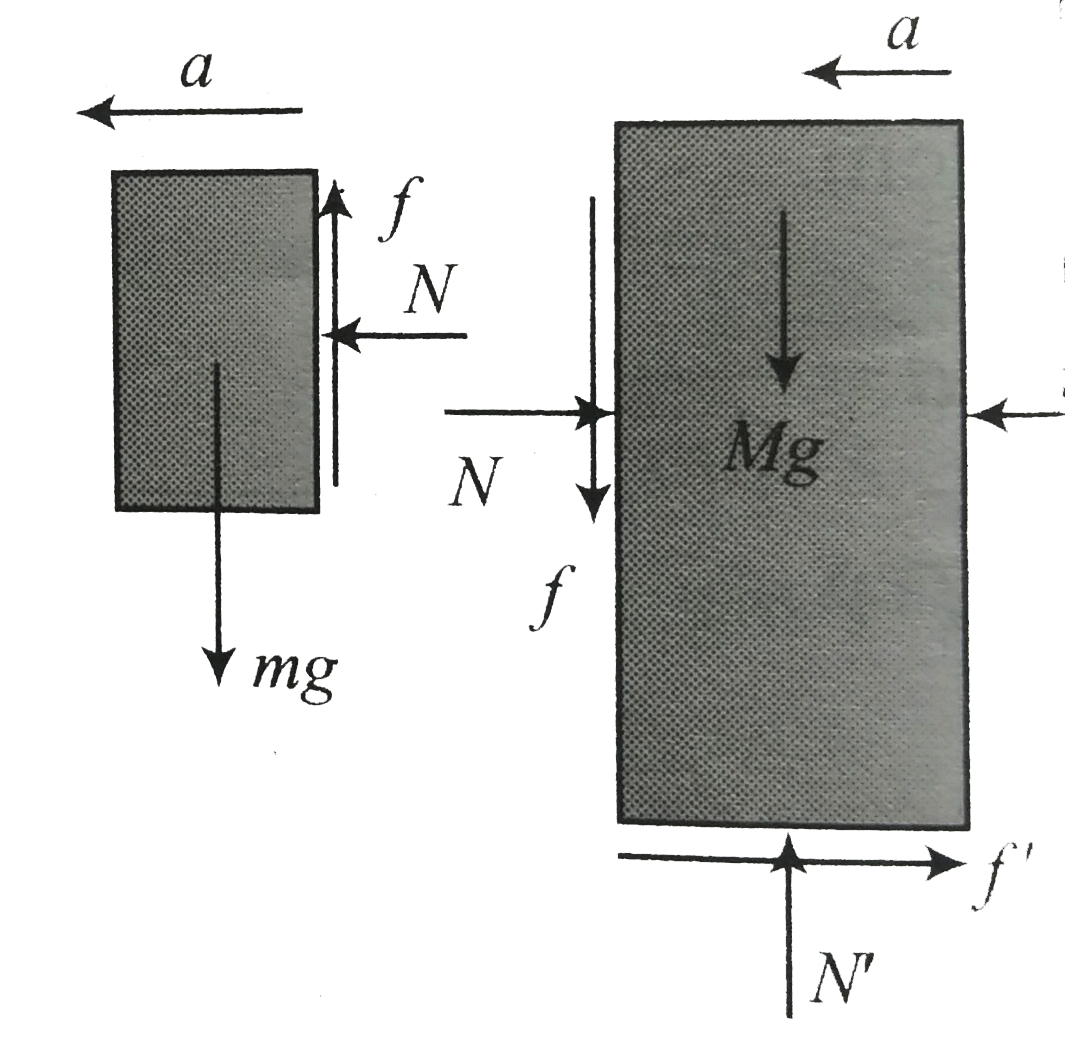
Equation of motion for `m`:
`sum F_(x) = ma rArr N = ma`
`sum F_(y) = 0 `
`FBD` of `m` and `M`
Since `m` is at rest relation to `M` at the verge of slipping.
`rArr f = mg`
Taking `''m` and `M''` together as system,
`f = mu N = mu(m + M)g`
`F - f' = (M + m)a`
`rArr a = (Fmug(M + m))/(M + m)`
`f le f_("max")`
`rArr mg le mu N`
`rArr mg le mu ma`
`rArr g le mu (F - mu (M + m))/(M +m)`
`rArr (M + m)g le mu F - mu^(2)g(M + m)`
`mu^(2)g (M + m) - mu F + (M + m)g le 0`
`rArr 2 mu^(2) - 5mu + 2 le 0`
For critical` 2muZ^(2) - 5 mu + 2 = 0`
`(mu - 2) (2 mu - 1) = 0`
`:. mu = 2` or `1//2`
Practically `mu` does not because `2` Therefore , `mu = 0.5`