Two wires `AC and BC` are tied at `C` of small sphere of mass `5kg ` which revolves at a constant speed `v` in the horizontal circle of radius `1.6 m ` Find the maximum value of `v`

Explanation

From force diagram shown in Fig
`T_(1) cos 30^(@) + T_(2) cos 45^(@) = mg`….(i)
`T_(1) sin 30^(@) + T_(2) sin 45^(@) = (mv^(2))/(r )`….(ii)
After solving Eqs. (i) and (ii)
`T_(1) = (mg - (nv^(2))/(r ))/(((sqrt(3) -1))/(2))`

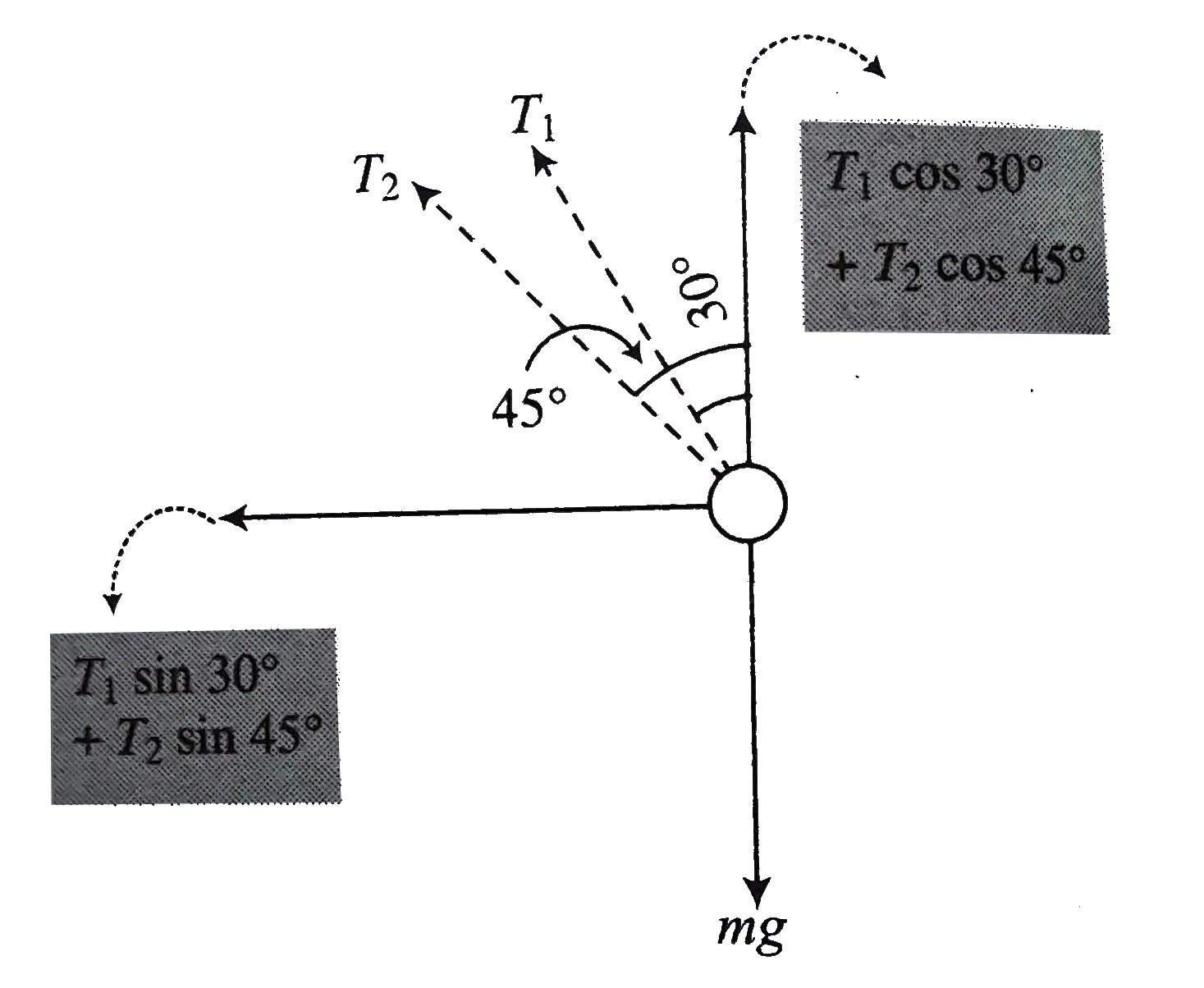
But `T_(1) gt 0 , = (mg - (nv^(2))/(r ))/((sqrt(3) -1)/(2)) gt 0 rArr mg gt (mv^(2))/(r ) lt
`rArr v ltsqrt (rg)`
`v_(max) = sqrt(rg) = sqrt(1.6 xx 9.8 ) = 3.96 ms^(-1)`