Angle of banking for designed speed
`tan theta = (upsilon_(0)^(2))/(Rg)` …(i)
`V = 36 kmh^(-1) = 10 ms^(-1)`
`rArr tan theta = (upsilon_(0)^(2))/(Rg)= (10^(2))/(20 xx 10) = (1)/(2)`
The vehicle may have the tendency to slide up or down depending on the speed of the vehicle .If speed of the vehicle is more it has tendency ti side up and vise- versa
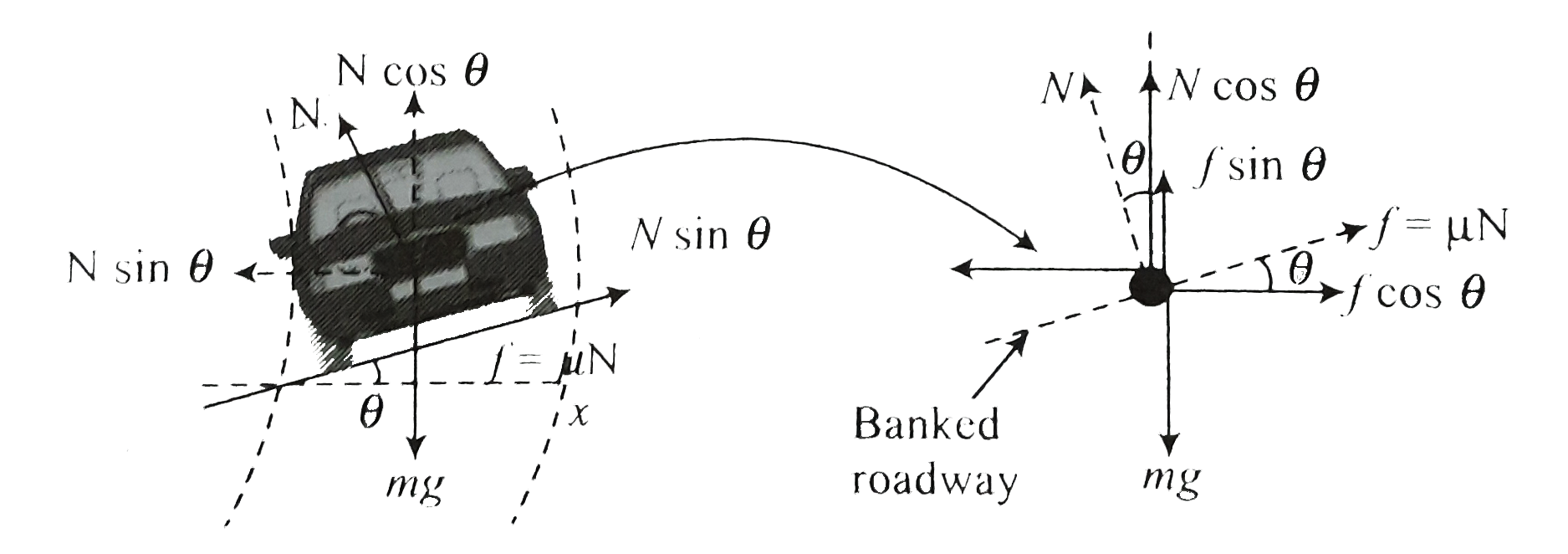
For speed graeter than designed speed : The vehicle has the tendecy to slide . friction will act downward.

In verticle direction `sum F_(y)= 0, N cos theta - mu N sin theta = mg `
In horizontal direction `sum F_(r)= (mv_(max)^(2))/(R )`
`N sin theta + mu N cos theta = (mv_(max)^(2))/(R )`....(i)
`N cos theta - mu N sin theta = mg`....(iii)
From (ii) and) (iii)
`(N (sin theta + mu cos theta))/(N (cos theta - mu sin theta)) = ((mv_(max)^(2))/(R ))/(mg) rArr ((sin theta + mu cos theta))/(cos theta - mu sin theta) = (v_(max)^(2))/(Rg)`
`rArr ((tan theta + mu)/(1 - mu tan theta)) = (v_(max)^(2))/(Rg)`....(iv)
`rArr ((tan theta + mu)/(1 - mu tan theta)) = ((0.5 + 0.4)/(1 - 0.4 xx 0.5))= (v_(max)^(2))/(20 xx 10)`
`rArr v_(max) = 15 ms^(-1)`
For speed less than desigram speed : The vehicle has tendecy to slide down friction will act upward
In verticle direction `sum F_(y)= 0, N cos theta + mu N sin theta = mg `....(v)
In horizontal direction `sum F_(r)= (mv_(max)^(2))/(R )`
`N sin theta - mu N cos theta = (mv_(max)^(2))/(R )`....(vi)
From (v) and) (vi) we get`((sin theta - mu cos theta))/(cos theta + mu sin theta)= (upsilon^(2))/(Rg)`
`((tan theta - mu)/(1 + mu tan theta )) = (upsilon^(2))/(Rg) rArr upsilon_(min)= 10 sqrt((1)/(6))ms^(-1)`