A coin is pushed down tangentially from an angular position `theta ` on a cylindrical surface , with a velocity `v` as shown in figure If the coefficient of friction the coin and surface is `mu` find the tangential acceleration of the coin

Explanation

As the coin slides down, friction is kinetic and acts up along tha plane

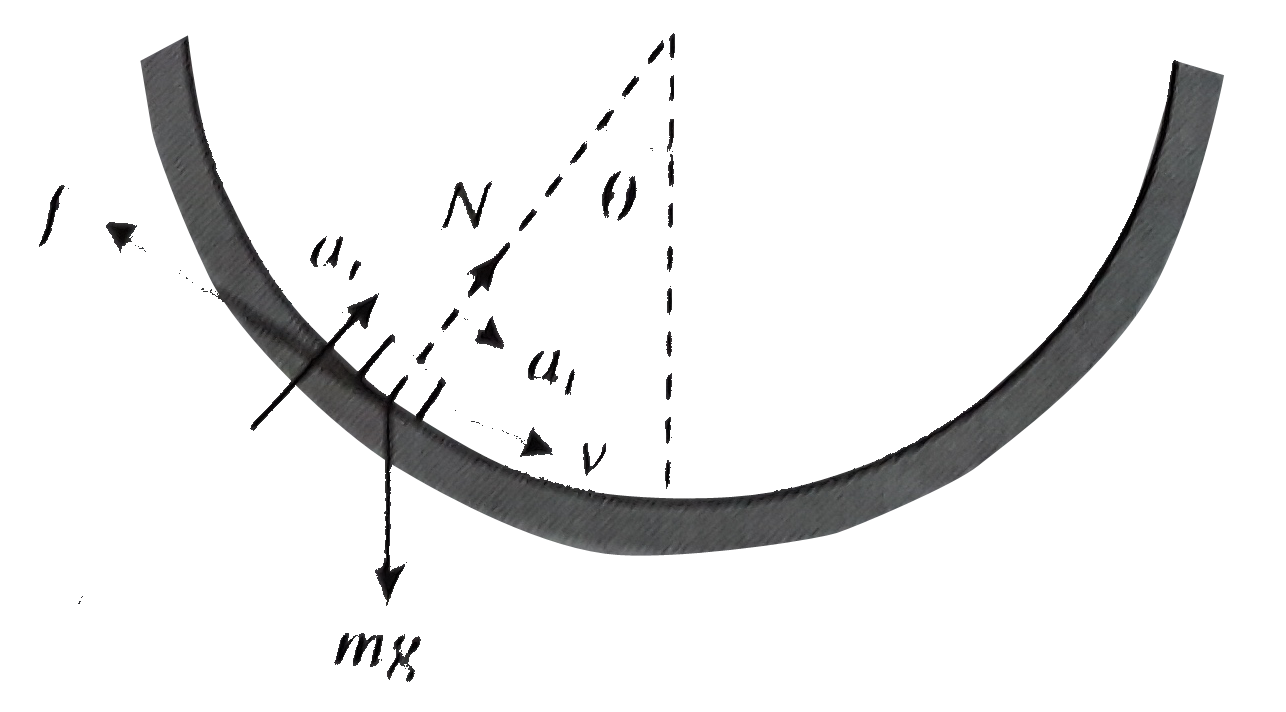
Equation of motion
`sum F_(r) = N - mg cos theta = ma_(r)`
`sum F_(t) = mg sin theta - f_(k) = ma_(1)`
` But f_(k) = mu N`
And centripetal acceleration is `a_(r) = (v^(2))/(R)`
Substituting `f_(k) ` from Eq (iii) and `a_(r) ` from Eq (iv) , in Eq we get
`a_(r) = g sin theta - (mu N)/(m)`
Now substituting `N` from Eq (i) in Eq (v) we get
` a_(t) = g(sin theta - mu cos theta ) - (mu v^(2))/(R )`