A particle of mass `m` is moving with a constant speed `v` in a circular path in a smooth horizontal plate (plan of the paper ) by a spring force as shown in figure If the natural length of the spring is `l_(0)` and stiffeness of the spring is `k` find the elongation of the spring

Explanation

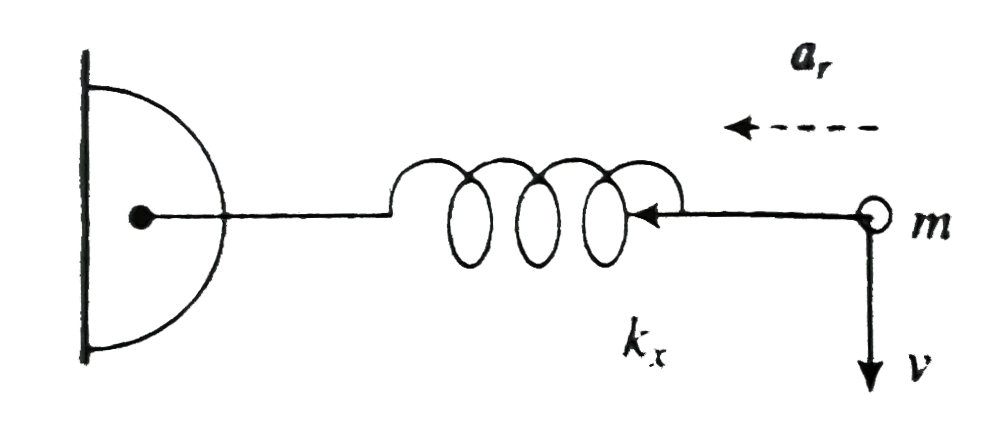
If the particle executes uniform circular motion , its speeds must be uniform because there is no tangential force to speed it up . Here the spring force `kt` acting on the particlein the centripetal force caused by the elongation `x` of the spring

Equation of motion
`sum F_(r) = F_(SP) = ma_(r)`
But centripental acceleration
`a_(r) = (v^(2))/(R)` (where `R =` radius of circular path)
Radius os rotation `R = 1_(0) + x`
`|F_(SP)| = kx`
Put in (i)` kx = (mv^(2))/((1_(0) + x)) rArr kx^(2) + kl_(0) x - mv^(2) = 0`
This given `x = (sqrt(k^(2)1_(0)^(2) + 4 mv^(2) k - kl_(0)))/(2k)`