Home
Class 11
PHYSICS
In fig two block of mass m(A) and m(B) a...

In fig two block of mass `m_(A) and m_(B)` are rotating at radius `r` kept on a rough table consider friction `(mu)` between all the contact surface pulley is frictionless determine the angular speed of the turn table for which the blocks just begin to slide

Text Solution

Verified by Experts

Equation for block `B` :
`sum F_(x) = T + mu_(s) m_(A) + m_(B) g + mu_(s)m_(A)g - m_(B) r omega^(2) = 0 `

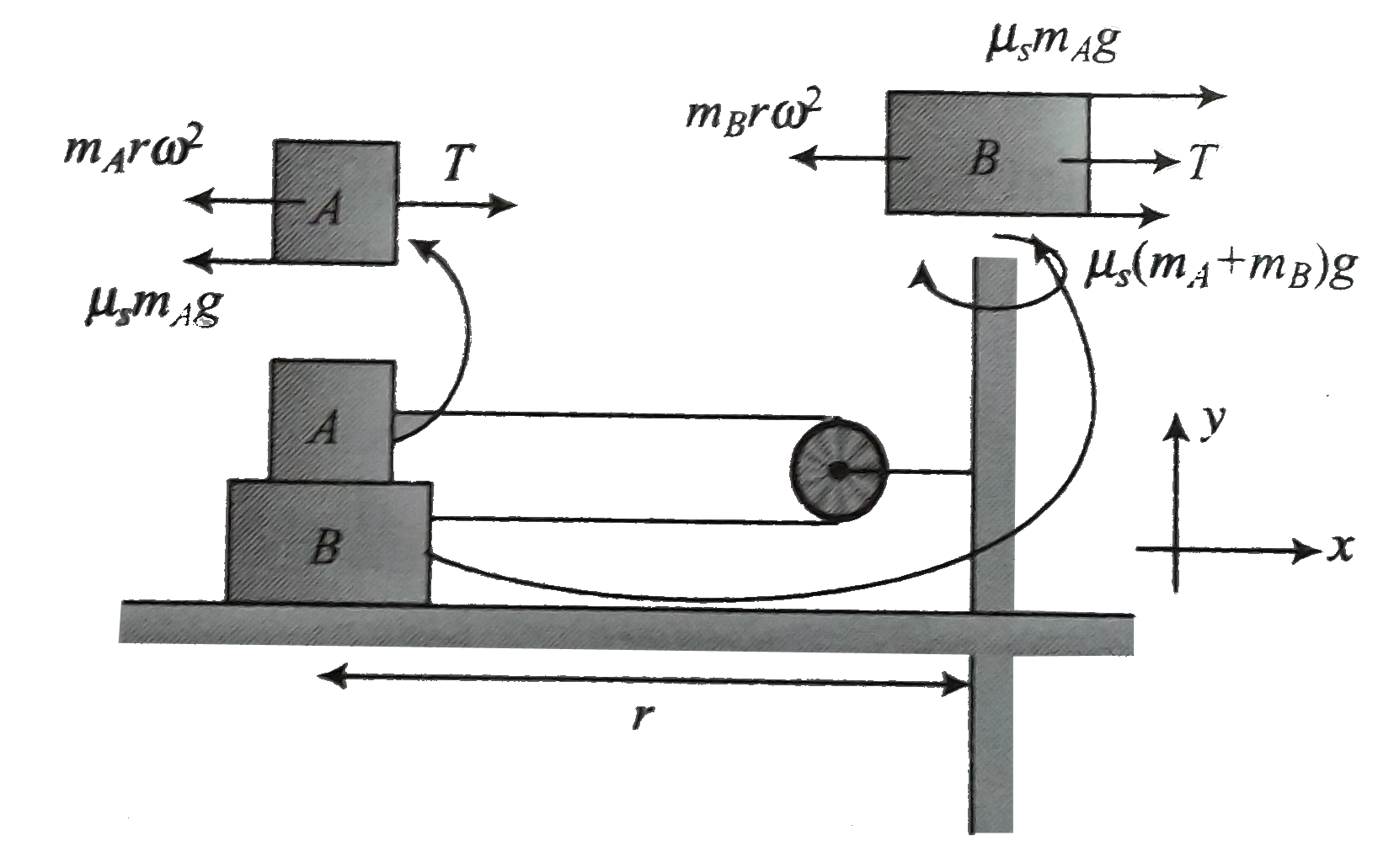
Equation for block `A` :
`sum F_(x) = T - mu_(s) (m_(A)) g - (m_(A)r omega^(2)) = 0` ...(i)
From equation (i) and (ii) , we climinate `T` as obtain
`2mu_(s) m_(A) g +mu(m_(A) - m_(B)) = (m_(B) - m_(A)) r omega^(2)`
`omega = [(mu_(s)g(3m_(A) + m_(B)))/(r(m_(B) - m_(A)))]^(1//2)`
Promotional Banner

Topper's Solved these Questions

  • NEWTON'S LAWS OF MOTION 2

    CENGAGE PHYSICS|Exercise Solved Examples|12 Videos

  • NEWTON'S LAWS OF MOTION 2

    CENGAGE PHYSICS|Exercise Exercise 7.1|25 Videos

  • NEWTON'S LAWS OF MOTION 1

    CENGAGE PHYSICS|Exercise Integer|5 Videos

  • PROPERTIES OF SOLIDS AND FLUIDS

    CENGAGE PHYSICS|Exercise INTEGER_TYPE|2 Videos

Similar Questions

Explore conceptually related problems

In Fig. shown two blocks are kept on a rough table, where m_(A)=0.9 kg, m_(B)=1.7 kg, r=13 cm, mu_(s)=0.1 . Consider friction between all the contact surface, pulley is frictionless. Determine the angular speed of the turn-rable for which the blocks just begin to slide

A block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is mu , then maximum angular speed of the table so that block does not slip

A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?

A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is mu . Then

A disc of mass m and radius R rotating with angular speed omega_(0) is placed on a rough surface (co-officient of friction =mu ). Then

Two blocks of masses m_(1) and m_(2) are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is mu . Find the minimum constant force F to be applied to m_(1) in order to just slide the mass m_(2) .

A block is kept on a horizontal table that is executing simple harmonic motion of frequency v in the horizontal plane. The coefficient of static friction between the block and the table is mu . Determine the maximum amplitude of the table for which the block does not slip on the surface of the table.

Two block of masses m and M are connected by a chord passing around a frictionless pulley which is attached to a rotating frame , which rotates about a vertical axis with an angular velocity omega If the coefficient of friction between the two masses and the surface are mu_(1) and mu_(2) respectively determine the value of omega at which the block starts sliding radially (M gt m)

A block m_(1) , strikes a stationary blocks m_(3) inelastically. Another block m_(2) , is kept on m_(3) . Neglecting the friction between all contacting surfaces, the fractional decrease of KE of the system in collision is