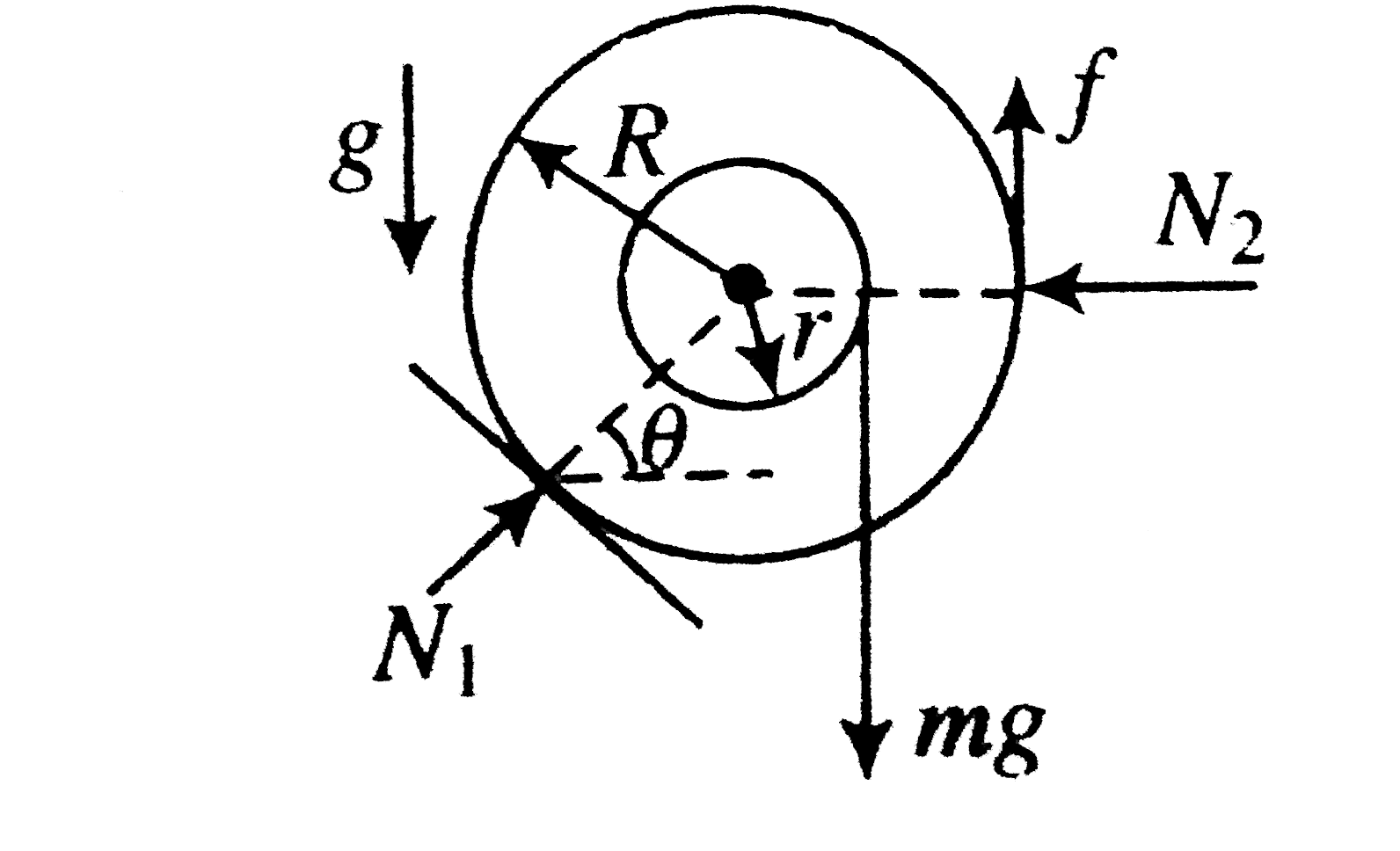A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
RIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Linked Comprehension|28 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Integer|11 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Single Correct|97 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS|Exercise INTEGER_TYPE|2 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Interger|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-RIGID BODY DYNAMICS 1-Multiple Correct
- A rigid body is in pure rotation, that is, undergoing fixed axis rotat...
Text Solution
|
- The moment of inertia of a thin square plate ABCD, fig, of uniform thi...
Text Solution
|
- A bucket of water of mass 21 kg is suspended by a rope wrapped around ...
Text Solution
|
- A massless spool of inner radius r outer radius R is placed against a ...
Text Solution
|
- A uniform thin flat isolated disc is floating in space. It has radius ...
Text Solution
|
- A rod bent at right angle along its centre line is placed on a rough h...
Text Solution
|
- A clockwise torque of 6N-m is applied to the circular cylinder as show...
Text Solution
|
- Illustrated is a uniform cubical block of mass M and side a Mark the c...
Text Solution
|
- The radius of gyration of a body depends upon
Text Solution
|