Home
Class 11
PHYSICS
A uniform sphere of mass m and radius r ...

A uniform sphere of mass `m` and radius `r` rolls without sliding over a horizontal plane, rotating ahout a horizontal axle `OA`. In the process, the centre of the sphere moves with a veocity `v` along a circle of radius `R`. Find the kinetic energy of the sphere.

Text Solution

Verified by Experts

Here the motion of the body is oribital and spin combined. The sphere is spining about a horizontal axis and orbiting about a vertical axis.
We write total kinetic energy of the sphere i.e.,
`KE=K_("orbital")+K_("spin")`

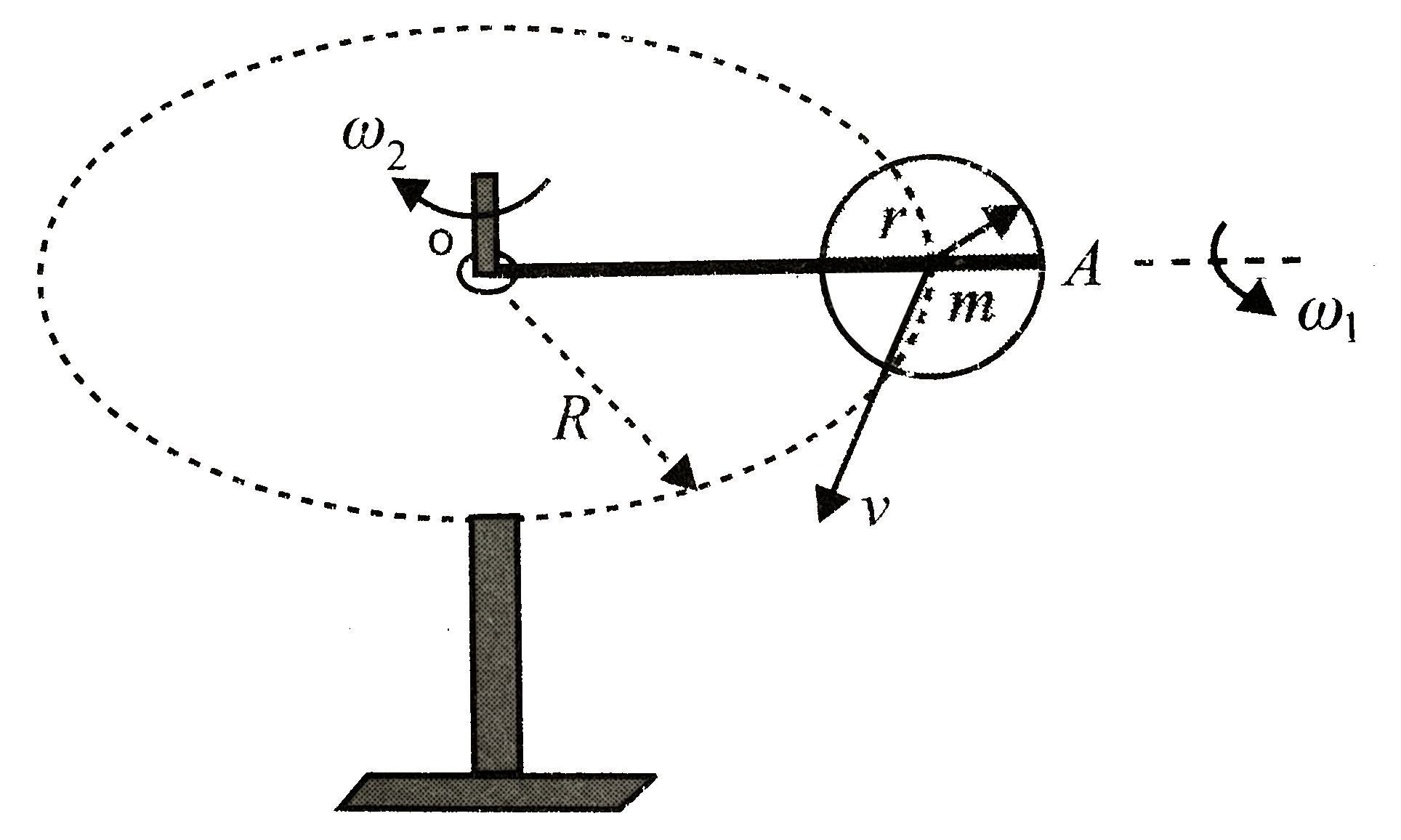
The kinetic energy of the sphere due to its rotation about its own axis nad its motion along circular path with velocity `v`.
`KE=1/2I_(1)omega_(1)^(2)+1/2I_(2)omega_(2)^(2)`
where `I_(1)=2/5mr^(2)` and `I_(2)=(2/5mr^(2)+mR^(2))`
`omega_(1)=v/r` and `omega_(2)=v/R`
Substituting these values in the above equation, we get
`KE=(7m)/10 v^(2)[1+(2r^(2))/(7R^(2))]`
Promotional Banner

Topper's Solved these Questions

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Solved Examples|12 Videos

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Exercise 3.1|11 Videos

  • RIGID BODY DYNAMICS 1

    CENGAGE PHYSICS|Exercise Integer|11 Videos

  • SOUND WAVES AND DOPPLER EFFECT

    CENGAGE PHYSICS|Exercise Integer|16 Videos

Similar Questions

Explore conceptually related problems

A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that v_(c.m.)=v_(0) .

A uniform sphere of mass m and radius R starts rolling without slipping down an inclined plane at an angle alpha to the horizontal. Find the time dependence of the angular momentum of the sphere relative to the point of contact at the initial moment. How will the obtained result change in the case of a perfectly smooth inclined plane?

A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is

A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is

A solid sphere of mass m rolls down an inclined plane a height h . Find rotational kinetic energy of the sphere.

A uniform sphere of mass m and radius R rolls without slipping down an inclined plane set at an angle theta to the horizontal. Find ( a ) the friction coefficient at which slipping is absent, ( b ) the kinetic energy of the sphere t seconds after the beginning of motion.

A uniform sphere of mass m and radius r rolls without slipping down a inclined plane, inclined at an angle 45^(@) to the horizontal . Find the magnitude of frictional coefficient at which slipping is absent :

If a solid sphere of mass 1kg and radius 0.1 m rolls without slipping at a unifrom velocity of 1 ms^(-1) along a stright line on a horizontal floor, the kinetic energy of the sphere is

If a solid sphere of mass 1 kg and radius 0.1 m rolls without slipping at a uniform velocity of 1 m/s along a straight line on a horizontal floor, the kinetic energy is