A rod of mass `m` and length `l` is connected with a light rod of length `l`. The composite rod is made to rotate with angular velocity `omega` as shown in the figure. Find the

a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.

Explanation

a. Translation kinetic energy of rod,

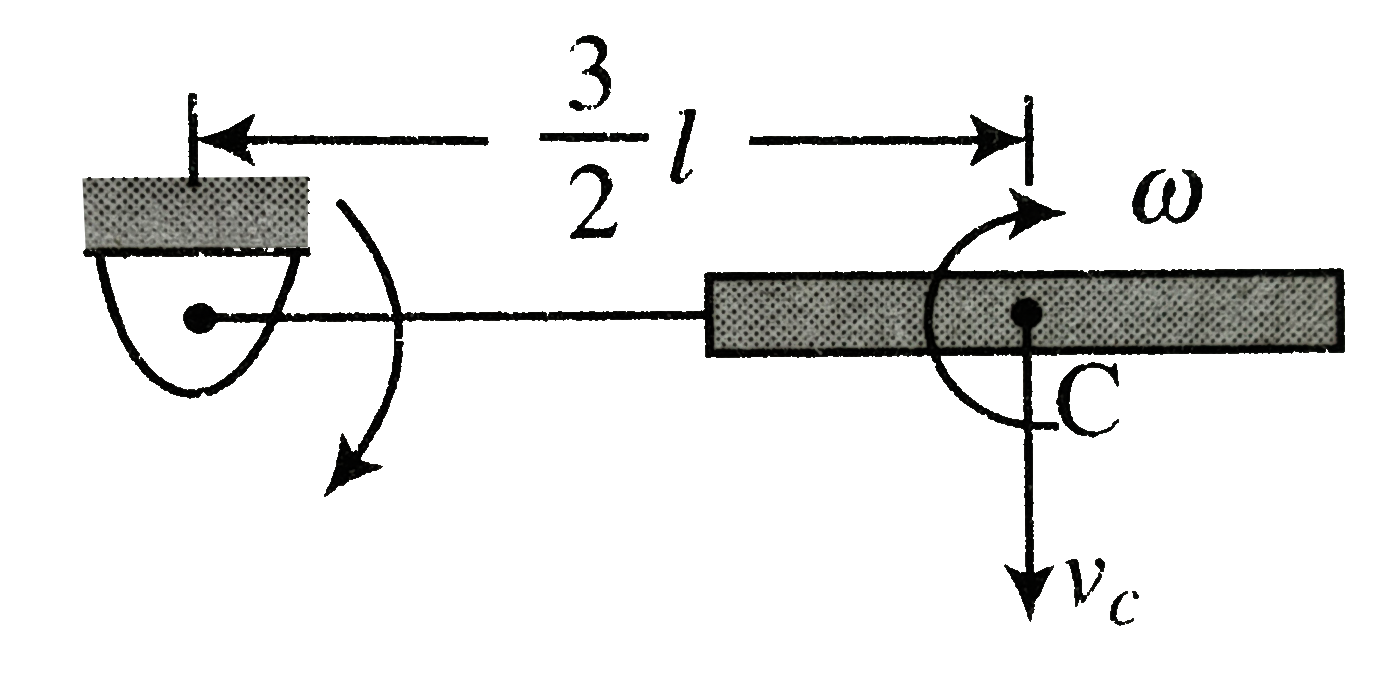
`K_("translational")=1/2mv_(c)^(2)`
Velocity of centre of mass `v_(C)=omega(3/2l)`
Hence `K_("translational")=1/2m[(3omegal)/2]^(2)=9/8momega^(2)l^(2)`
b. rotational kinetic energy of rod
`K_("rotational")=1/2I_(C)omega^(2)=1/2[(ml^(2))/12]omega^(2)=1/24momegal^(2)`
c. Total kinetic energy
`K_("total")=K_("translational")+K_("rotational")`
`9/8momega^(2)l^(2)+1/24momega^(2)l^(2)=7/6momega^(2)l^(2)`