Two beads each of mass `m` are welded at the ends of two light rigid rods each of length `l`. if the pivots are smooth, find the ratio of translational and rotational kinetic energy of system.

Explanation

We know transltional kinetic energy `K_(r)=1/2I_(C)omega^(2)`
Distance of centre of mass from pivot end

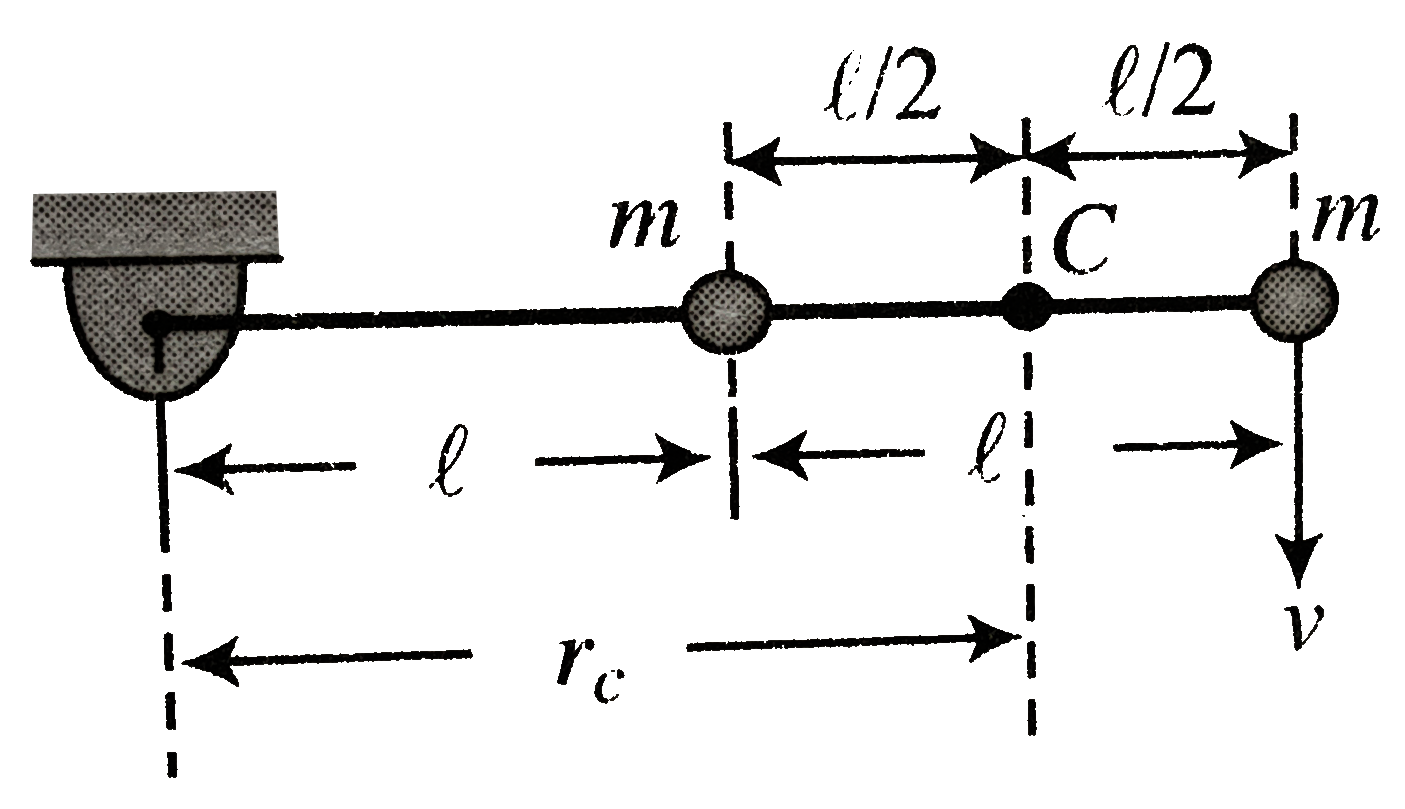
`r_(C)=(ml+m(2l))/(m+m)=3/2l`
Moment of inertia of system about centre of mass
and `I_(C)=m(l/2)^(2)+m(l/2)^(2)=(ml^(2))/2`
Angular velocity of rod `omega=v/(2l)`
velocity of centre of mass
`v_(cm)=omega(3/2l)=(v/(2l))(3/2l)=3/4v`
Translation kinetic energy of system
`K_("translation")1/2M_("total").v_(cm)^(2)=1/2(2m)(3/4v)(2)=9/16mv^(2)`
`K_("rotational")=1/2I_(CM)omega^(2)=1/2((ml)2)^(2)(v/(2l))^(2)=1/16mv^(2)`
this gives `(K_(r))/(K_(r))=9`