A uniform rod of mass `m` and length `l` is pivoted smoothly at `O`. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation `theta.`
b.What is the maximum angular displacement of the rod?

Explanation

a. Using work energy theorem `W_(F)+W_(gr)=/_\K`

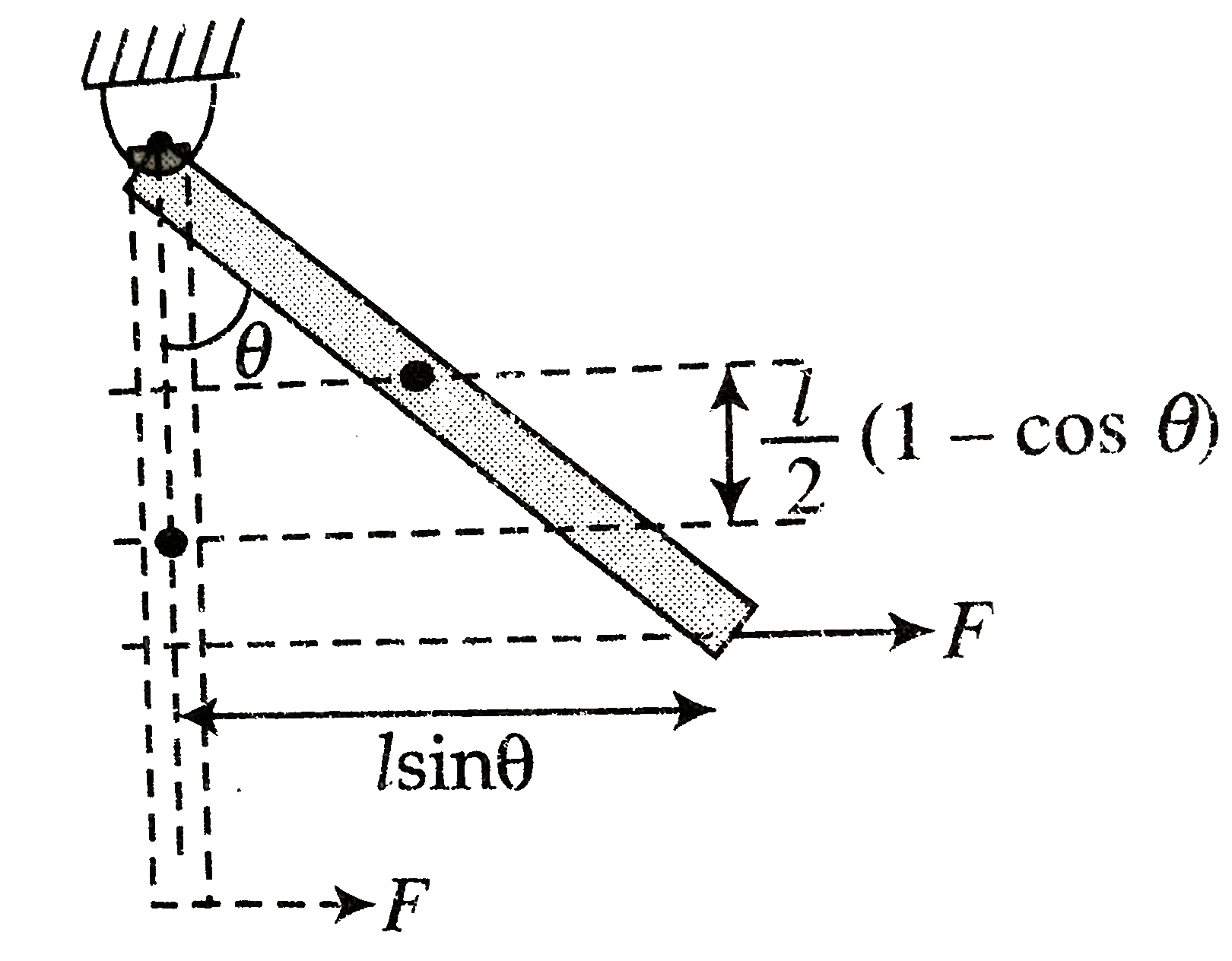
`Flsintheta-mgl/2(1-costheta)-1/2((ml^(2))/3)omega^(2)`
`omega=((6F)/(ml)sintheta-(3g)/(1-costheta))`
b. At maximum angular displacement put `omega=0` in eqn
`0=sqrt((6E)/(ml)sintheta-(3g)/(1-costheta))`
`implies(6E)/(ml)sintheta=(3g)/l(1-costheta)`
`implies (2E)/m(2(sintheta)/2.(costheta)/2)=g((2sin^(2)theta)/2)`
`implies tantheta/2=(2F)/(mg)implies theta=2tan^(-1)((2F)/(mg))`