Home
Class 11
PHYSICS
A solid cyinder of mass m=4 kg and radiu...

A solid cyinder of mass `m=4 kg` and radius `R=10 cm` has two ropes wrapped around it. one near each end. The cylinder is held horizontally by fixing the two free ends of the cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the linear acceleration of the cylinder.

Text Solution

Verified by Experts

Method 1: Force/Torque Method:
Let `a=` linear acceleration and `alpha=` angular acceleration of the cylinder. For the linear motion of the cylinder.
`mg-2T=ma`
For the rotational motion: Net torque `=Ialpha`

Also, the linear acceleration of the cyinder is the same as the tangential acceleration of an point its surface, `a=Ralpha`
Combining the three equations, we get
`mg=ma+m/2aimpliesa=2/3g`
Method 2: Energy method
The motion of the cylinder is rotational and translation combined . Using conservation of mechanical energy
`/_\K=/_\U=0`

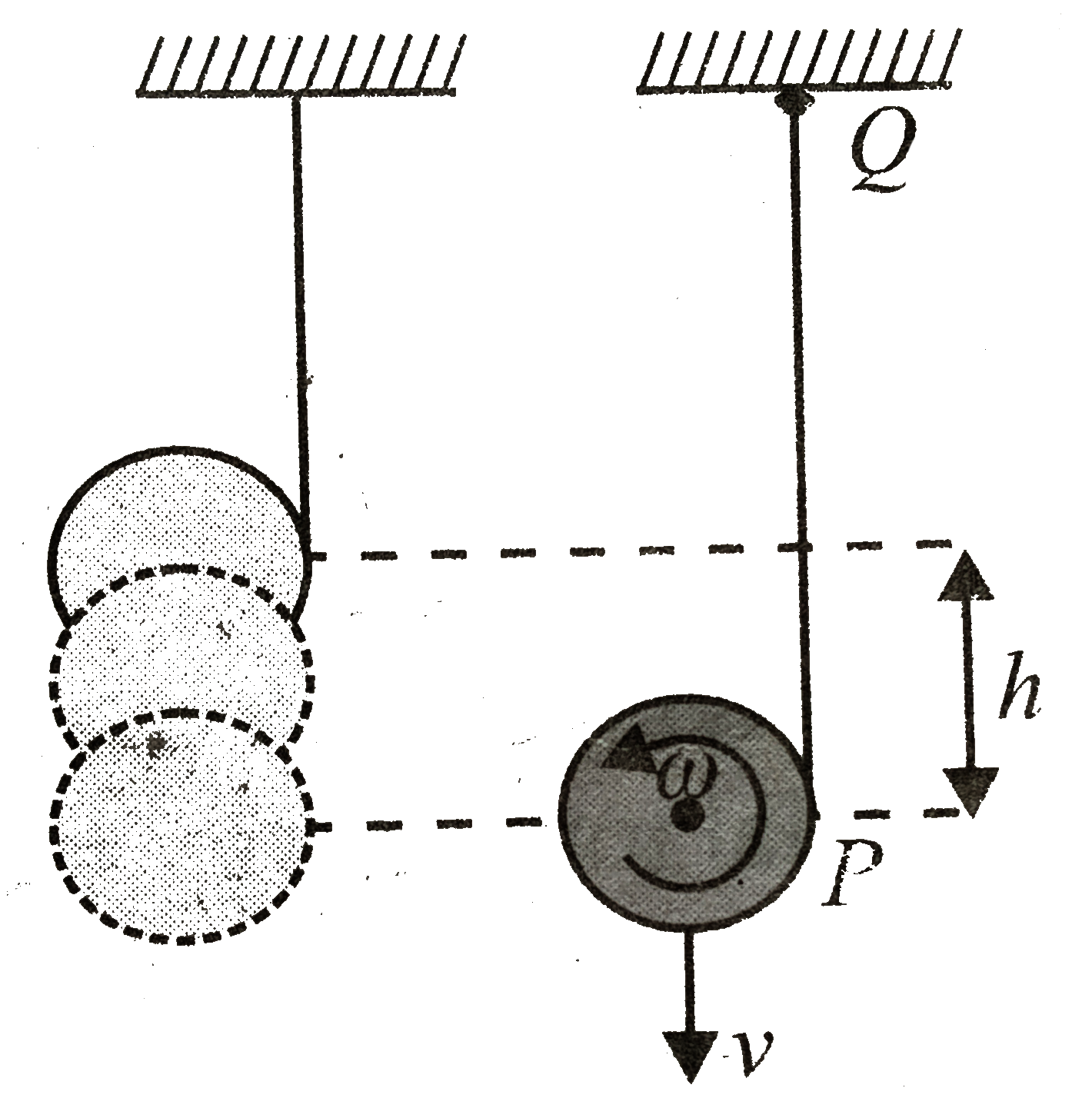
`/_\K+/_\U=0`
or Loss in `PE =` gain in `KE`
`mgh=1/2mv^(2)+1/2Iomega^(2)`
Constraint relation
Velocity of point `P v_(P)=0v-omegaR`
`omega=v/R` .........i
From eqn and i and ii `mgh=1/2mv^(2)+1/2((mR)/2(v/R)^(2)`
`=m/2 (v^(2)+(v^(2))/2)`
`2gh=3/2v^(2)implies v^(2)=4/3gh` ..... ii
Differentiating eqn iii with respect to time, we get
`2v(dv)/(dt)=4/3g(dh)/(dg)`
`22va=4/3gvimpliesa=2/3g`
Promotional Banner

Topper's Solved these Questions

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Solved Examples|12 Videos

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Exercise 3.1|11 Videos

  • RIGID BODY DYNAMICS 1

    CENGAGE PHYSICS|Exercise Integer|11 Videos

  • SOUND WAVES AND DOPPLER EFFECT

    CENGAGE PHYSICS|Exercise Integer|16 Videos

Similar Questions

Explore conceptually related problems

A solid cylinder of mass m=4kg and radius R=10cm has two ropes wrapped around it, one near each end. The cylinder is held horizontally by fixing the two free ends of he cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the tension along the strings.

A cylindrical rod of mass M , length L and radius R has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is : .

A cylinder of mass m suspended by two strings wrapped around the cylinder one near each end, the free ends of the string being attached to hooks on the ceiling, such that the length of the cylinder is horizontal. From the position of rest , the cylinder is allowed to roll down as suspension strings unwind , calculate (a) The downward linear acceleration of the cylinder (b) The tension in the strings (c) The time dependence of the instantaneous power developed by gravity

A scylindrical rod of mass M, length L & radius R has cords wound around it , whose ends are attached to the ceioling .The rod is held borizontal and released .The liinear acceleration of the cylinder as it falls and tension in the cords is

A solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'

A plank of mass M , is placed on a smooth surface over which a cylinder of mas m(=M) annd radius R=1m is placed as shown in figure. Now the plane is pulled towards the right wilth an external force F(=2Mg) . If the cyinder does not slip over the surfcace of the plank, find the linear acceleration of he plank and the cylinder and the angular acceleration of the cylinder. (Take g=10 ms^(2) )

A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure. (a). Show that the acceleration of the cylinder is downward with magnitude a=(2g)/(3) (b). Find the tension in the string.

A uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table. Angular acceleration of the cylinder is

A cord is wound round the circumference of a solid cylinder radius R and mass M . The axis of the cylinder is horizontal. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h .

A uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?