Home
Class 11
PHYSICS
A particle is projected at time t=0 from...

A particle is projected at time t=0 from a point P wilth a speed `v_0` at an angle of `45^@` to the horizontal. Find the magnitude and the direction of the angular momentum of the parallel about the point P at time `t=v_0/g`

Text Solution

Verified by Experts

Let us take the origin at `P,x`-axis along the horizonntal and `y`-axis along the vertically upward direction as shown in figure.

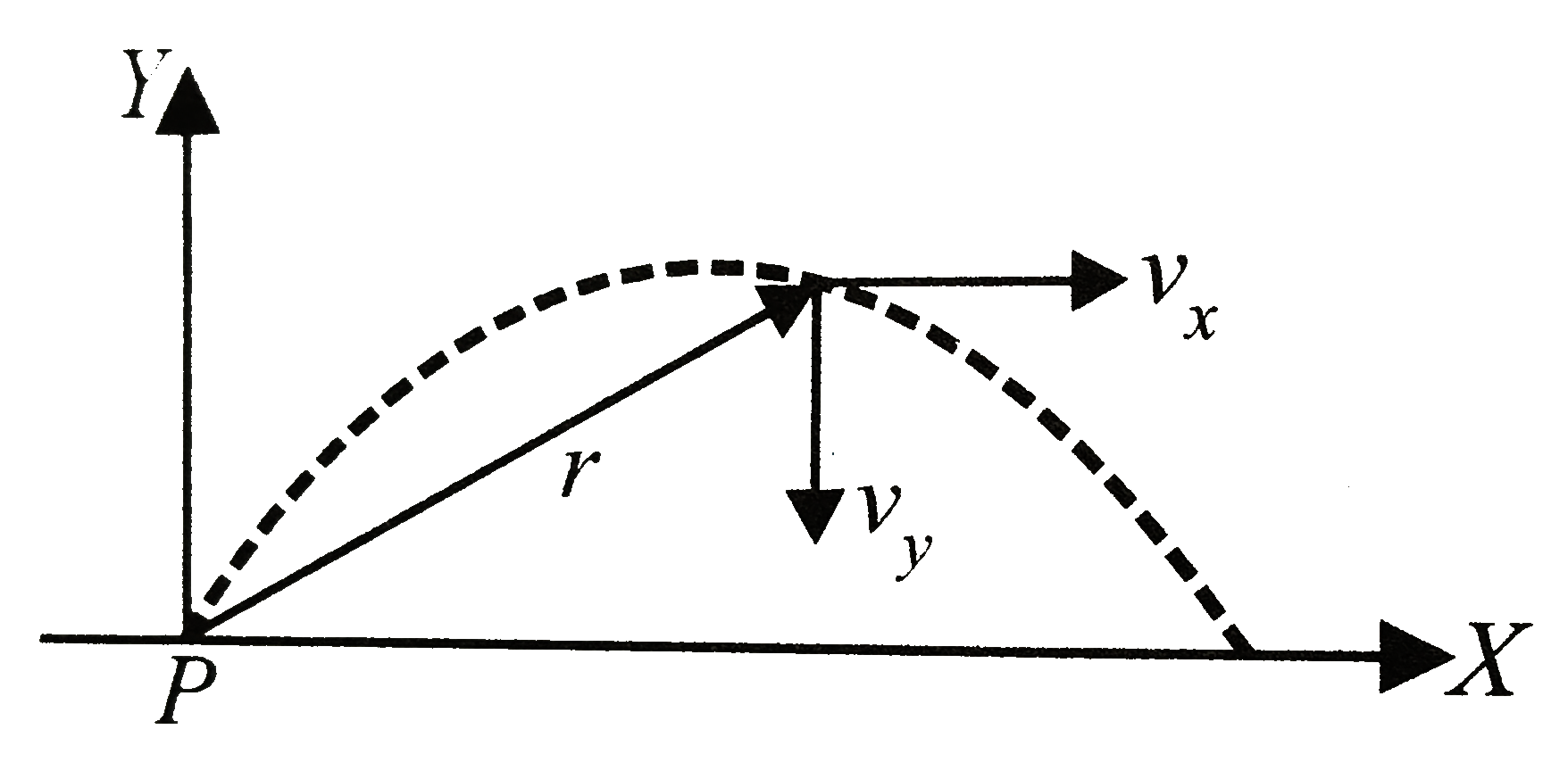
For horizontal motion during the thime `0` to `t`,
`v_(x)=v_0cos45^@=(v_(0))/(sqrt(2))`
and `x=v_(x)t=(v_(0))/(sqrt(2)) (v_(0))/g=(v_(0)^(2))/(sqrt(2)g)`
For vertical motion using `v_(y)=v_(sigmay)-"gt"`
`v_(y)=v_(0)sin45^@-g((v_(0))/g)=((1-sqrt(2)))/sqrt(2)v_(0)`
and `y=(v_(0)sin45^@)t-1/2"gt"^(2)`
`implies y=(v_(0))/(sqrt(2))(v_(0))/g)-1/2g((v_(0))/g)^(2)=(v_(0)^(2))/(2g) sqrt(2-1)`
The angular momentum of the particle at time `t` about the origin is
`L=vecrxxvecp=m(vecrxxvecv)`
`=(vecix +vecjy)xx(v_(x)veci+v_(y)vecj)=m(veckxv_(y)-veckyv_(x))`
`=mveck[((v_(0)^(2))/(sqrt(2)g))(v_(0))/sqrt(2)(1-sqrt(2))-(v_(0)^(2))/(2g)(sqrt(2)-1)(v_(0))/(sqrt(2))]`
`=-veck(mv_(0)^(3))//(2sqrt2g)`
Thus, the angular momentum of the particle is `mv_(0)^(3)//(2sqrt(2)g)` in the negative `Z`-direction, i.e., perpendicular to the plane of motion going into the plane.
Promotional Banner

Topper's Solved these Questions

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Solved Examples|12 Videos

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Exercise 3.1|11 Videos

  • RIGID BODY DYNAMICS 1

    CENGAGE PHYSICS|Exercise Integer|11 Videos

  • SOUND WAVES AND DOPPLER EFFECT

    CENGAGE PHYSICS|Exercise Integer|16 Videos

Similar Questions

Explore conceptually related problems

A particle is projected at time t=0 from a point P on the ground with a speed v_0, at an angle of 45^@ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem t= v_0//g

A particle is projected at time t=0 from a point (P) with a speed v_(0) at an angle of 45^(@) to the horizontal.The magnitude of angular momentum of the particle about the point (P) at time (t=(v_(0))/(g)) is (mv_(0)^(3))/(2g sqrt(X)) .Then the value of X is?

A particle of mass m is projected at t=0 from the point P on the ground with speed v_(0) at an angle of theta to the horizontal. Find the magnitude and direction of the angular momentum of the particle at time t=(v_(0)sintheta)/(2g) .

A particle is projected at time t=0 from a point O with a speed u at an angle theta to horizontal. Find the torque of a gravitational force on projectile about the origin at time t. (x,y plane is vertical plane)

A particle of mass m is projected with a velocity v making an angle of 45^@ with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.

A particle is projected from a point P with a velocity v at an angle theta with horizontal. At a certain point Q it moves at right angles to its initial direction. Then

A particle of mass m is projected with a speed v_(0) at an angle of projection theta with horizontal. Find the torque of the weight of the particle about the point of projection after time (v_(0)sintheta)/(g)

A particle is projected with a speed v and an angle theta to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.