Home
Class 11
PHYSICS
A uniform disc of mas M and radius R is ...

A uniform disc of mas `M` and radius `R` is smoothly pivoted at `O`. A light inextensible string wrapped over the disc hangs a particle of mass `m`. If the system is released from rest, assuming that the string does not slide on the disc, find the angular speed of the disc as the function of time using impulse momentum equation.

Text Solution

Verified by Experts

The net torque about `O` is
`vectau=mgRhatk` ………i
The angular momentum of the disc particle system about `O` is `L=I_(0)omega+mvR`, where `v=Romega`
`L=(MR^(2))/2omega+mR^(2)omega=((MR^(2))/2+mR^(2))omega`

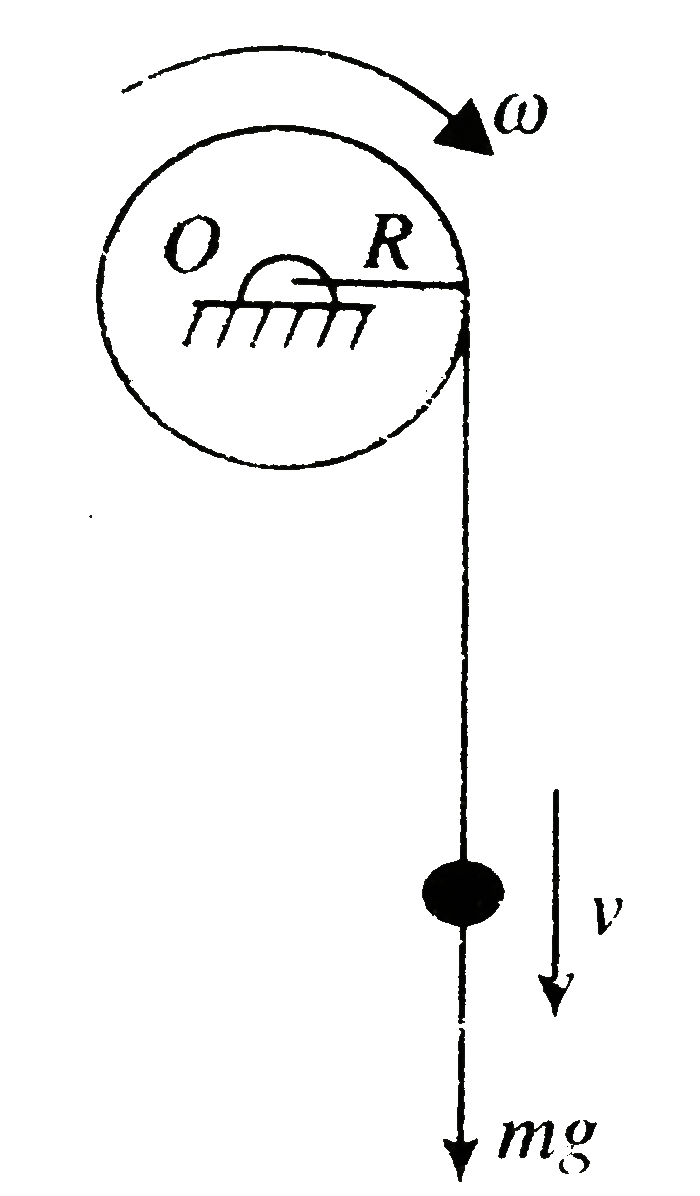
`vecL=((M+2m)/2)R^(2)omegahatk`.........ii
Impulse momentum equation is
`/_\vecOL=intvectau dt`
Using eqn i , ii and ii we have
`((M+2m)/2)R^(2)omega=mgRint_(0)^(1)dt`
`omega=(2m"gt")/((M+2m)R)`
Promotional Banner

Topper's Solved these Questions

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Solved Examples|12 Videos

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Exercise 3.1|11 Videos

  • RIGID BODY DYNAMICS 1

    CENGAGE PHYSICS|Exercise Integer|11 Videos

  • SOUND WAVES AND DOPPLER EFFECT

    CENGAGE PHYSICS|Exercise Integer|16 Videos

Similar Questions

Explore conceptually related problems

A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.

A mass less string is wrapped around a uniform disc of mass m and radius r . The string passes over a mass less pulley and is tied to a block of mass M at its other end (see figure). The system is released from rest. Assume that the string does not slip with respect to the disc. (a) Find the acceleration of the block for the case M = m (b) Find (M)/(m) for which the block can accelerate upwards.

A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is

A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

A uniform disc of mass M and radius R is supported vertically by a pivot at its periphery as shown. A particle of mass M is fixed to the rim and raised to the highest point above the center. The system is released from rest and it can rotate about pivot freely. The angular speed of the system when the attached object is directly beneath the pivot, is

A uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is

A disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

A uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is