Home
Class 11
PHYSICS
The two uniform discs rotate separately ...

The two uniform discs rotate separately on parallel axles. The upper disc (radius `a` and momentum of inertia `I_1`) is given an angular velocity `omega_0` and the lower disc of (radius `b` and momentum of inertia `I_2`) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
.

Text Solution

Verified by Experts

The two discs exert equal and opposite forces on each other when in contact. The torque due to these forces change the angular momentum of each disc. Form angular impulse angular momentum theorem, we have

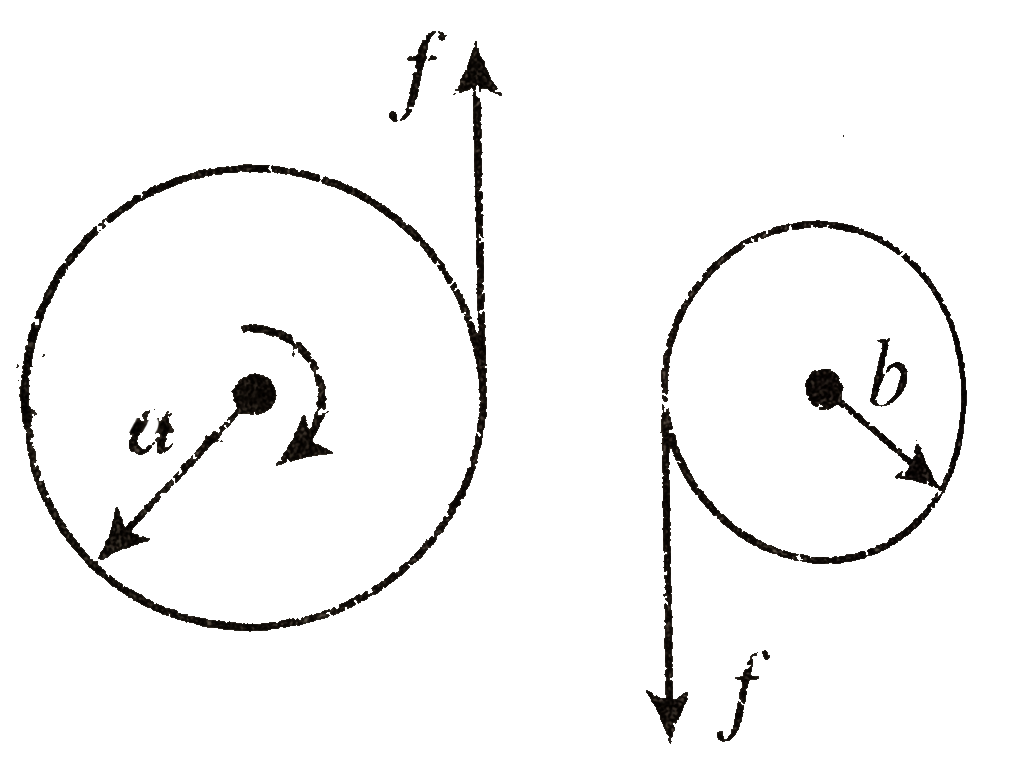
`fa/_\t=I_(1)(omega_(0)-omega_(1))`
and `fb/_\t=I_(2)omega_(2)`
From eqn i and ii we get
`a/b=(I_(1)(omega_(0)-omega_(1)))/(I_(2)omega_(2))`
When slipping ceaes between the disc, the contact points the two dics have the same linear velocity i.e.,
`aomega_(1)=bomega_(2)`
on substituting `omega_(2)` in eqn iii we get
`omega_(1)=((I_(1)omega_(0)))/([I_(1)+(a^(2)I_(2)//b^(2))])`
Promotional Banner

Topper's Solved these Questions

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Solved Examples|12 Videos

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS|Exercise Exercise 3.1|11 Videos

  • RIGID BODY DYNAMICS 1

    CENGAGE PHYSICS|Exercise Integer|11 Videos

  • SOUND WAVES AND DOPPLER EFFECT

    CENGAGE PHYSICS|Exercise Integer|16 Videos

Similar Questions

Explore conceptually related problems

A disc of moment of inertia I_(1) is rotating freely with angular speed omega_(1) when another non-rotating disc of moment of inertia I_(2) is dropped on it. The two discs then rotate as one unit. Find the final angular speed.

A disc rotates with angular velocity omega and kinetic energy E . Then its angular momentum

Initial angular velocity of a circualr disc of mass M is omega_1. The tow sphere of mass ma re attached gently to diametrically opposite points ont eh edge of the disc. What is the final angular velocity on the disc?

A disc of moment of inertia 3 kg m^(2) is acted upon by a constant torque of 60 Nm, if the disc is at rest, then the time after which the angular velocity of the disc is 90 rad/s, will be

A round disc of moment of inertia I_2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I_1 rotating with an angular velocity omega about the same axis. The final angular velocity of the combination of discs is.

Initial angular velocity of a circular disc of mass M is omega_(1) . Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -

A uniform disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to its plane with an angular velocity omega . Another disc of mass M/3 and radius R/2 is placed gently on the first disc coaxial. Then final angular velocity of the system is

A uniform circular disc of radius R is rotating about its own axis with moment of inertia I at an angular velocity omega if a denser particle of mass m is gently attached to the rim of disc than its angular velocity is

A child with mass m is standing at the edge of a disc with moment of inertia I , radius R m and initial angular velocity omega . See figure given below. The chlid jumps off the edge of the disc with tangential velocity v with respect to the ground. The new angular velocity of the disc is. .