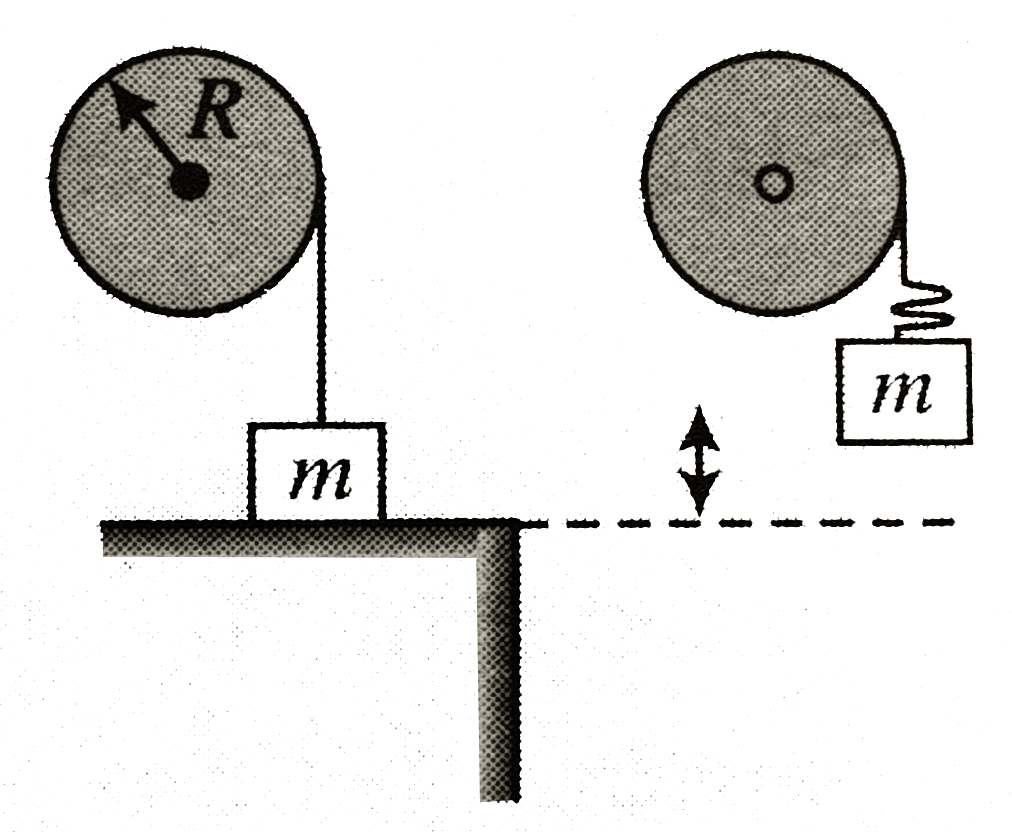A string is wrapped several times on a cylinder of mass `M` and radius `R`. the cylinder is pivoted about its adxis of block symmetry. A block of mass `m` tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance `h`, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity `omega_(0)` of the cylinder ,the speed `v_(0)` of the falling body, `m` and the kinetic energy `K_(0)` of the system.
b. Evaluate the corresponding quanitities `omega_(1), v_(1)` and `K_(1)` for the instant just after the string becomes taut.
c. Why is `K_(1)` less than `K_(0)`? Where does the energy go?
d. If `M=m`, what fraction of the kinetic energy is lost when the string becomes taut?

Explanation

a. Just before the stirng becomes taut, the block falls freely, so `v_(0)=sqrt(2gh),` There is no tension in the string so nothing causes the cylider to spin so `omega_(0)=0`. The kinetic energy of the system is `K_(0)=1/2mv_(0)^(2)+1/2lomega_(0)^(2)=mgh`.
b. When the string experiences a jerk, the large impulse developed of very short duration so that the contribution of weight `mg` can be neglected during this time interval. The angular momentum of the system is conserved, as the tension is internal force for the system. Thus we have
`vecL_(i)=vecL_(f)`
`mv_(1)R+1/2MR^(2)omega_(1)=mv_(0)R=msqrt(2gh)R`
The string is inextensible so `v_(1)=Romega_(1).` On solving for `omega_(1)`, we get ltbr `omega_(1)=sqrt((2gh))/(R[1+(M/2m)]),v_(1)=Romega_(1)=(sqrt(2gh)/([1+(M/2m)])`
The final kinetic energy `K_(1)` is given by
`K_(1)=1/2mv_(1)^(2)+omega_(1)^(2)`
`=1/2mv_(1)^(2)+1/2(1/2MR^(2))((v_(1)^(2))/R^(2))=1/2(m+M/2)v_(1)^(2)`
`=1/2[(mv_(0)^(2))/(1+(M/2m))]=(K_(0))/(1+(M/2m))`
c. The situation in this case is analogous to the energy loss is complete inelastic two body collisions. The lost kinetic energy is converted to heat energy or elastic potential energy of the string or in the two objects.
d.For `M=m, K_(1)=(2K_(0))/3,` so the fraction lost is
`((K_(0)-K_(1))/K_(0))=1/3`