Velcity of the centre `=v_(0)` and the angular velocity about the centre `=v_(0)//2r`. Thus `v_(0)gtomega_(0)r`. The sphere slips forward and thus the firction by the plane on the sphere will act backward. As the firction is kinetic, its value is `mu=muMg` and the sphere wil be decelerated by `a_(CM)=f/M`
`Hence, v(t)=v_(0)-f/Mt`...........i
This friction will also have a torque `= fr` about the centre. this torque is clockwise and in the direction of `omega_(0)`. Hence, the angular acceleration about the centre will be
`alpha=f r/((2/5)Mr^(2))=(5f)/(2Mr)`
`=(v_(0))/(2r)+(5)/(2Mr)t`
Pure rolling starts when `v(t)=romega(t)`,
i.e, `v(t)=(v_(0))/2+(5f)/(2M)t` ............ii
Eliminating `t` from eqn i and ii we get
`5/2v(t)+v(t)=5/2v_(0)+(v_(0))/2`
or `v(t)=2/7xx3v_(0)=6/7v_(0)`
Thus, the sphere rolls with translational velocity `6v_(0)//7` in the forward direction.
Alternative method: We can solve this problem by using conservation of angular momentum. We can conserve the angular momentum about any point situated on the ground. (as torque of friction for about any point on the ground is Zero).
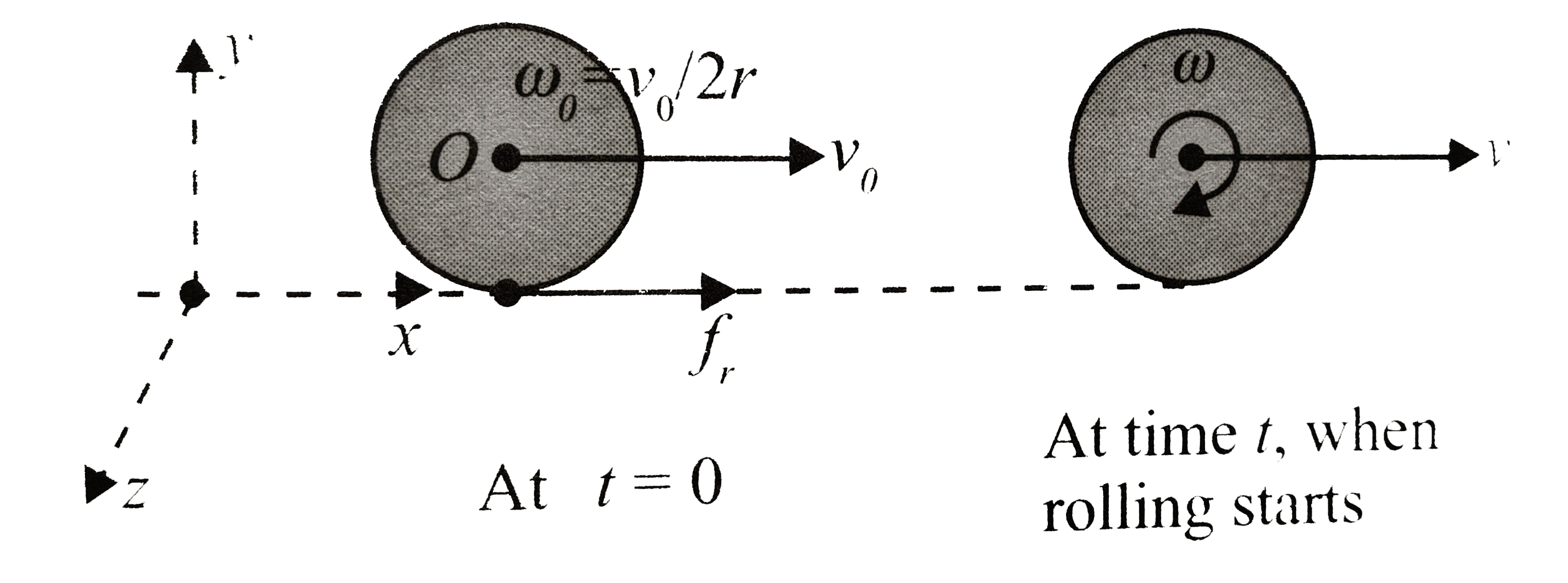
Angular momentum about any point `O` situated on ground at `t=0`
`vecL_("initial")=vecL_(CM)+vecrxxmvecv`
`=I_(CM)omega_(-hatk)+Mv_(0)r(-hatk)`
`=[2/5Mr^(2)((v_(0))/(2r))+Mv_(0)r](-hatk)`
`vecL_("initial")=6/5Mv_(0)(-hatk)`..........i
Angular momentum at time `t` when rolling starts
`vecL_("final")=vecL_(cm)+vecrxxmvecv=2/5mr^(2)omega(-hatk)+mvr(-hatk)`
When rolling starts`v=omegaR` or `omega=v/r`
Hence `vecL_("final")=[2/5mr^(2)(v/r)+mvr](-hatk)`
`=7/5mvr(-hatk)`........ii
Conserving angular momentum we get
`vecL_("initial")=vecL_("final")`
`6/5mv_(0)r(-hatk)=7/5mvr (-hatk)`
which gives `v=6/7v_(0)`