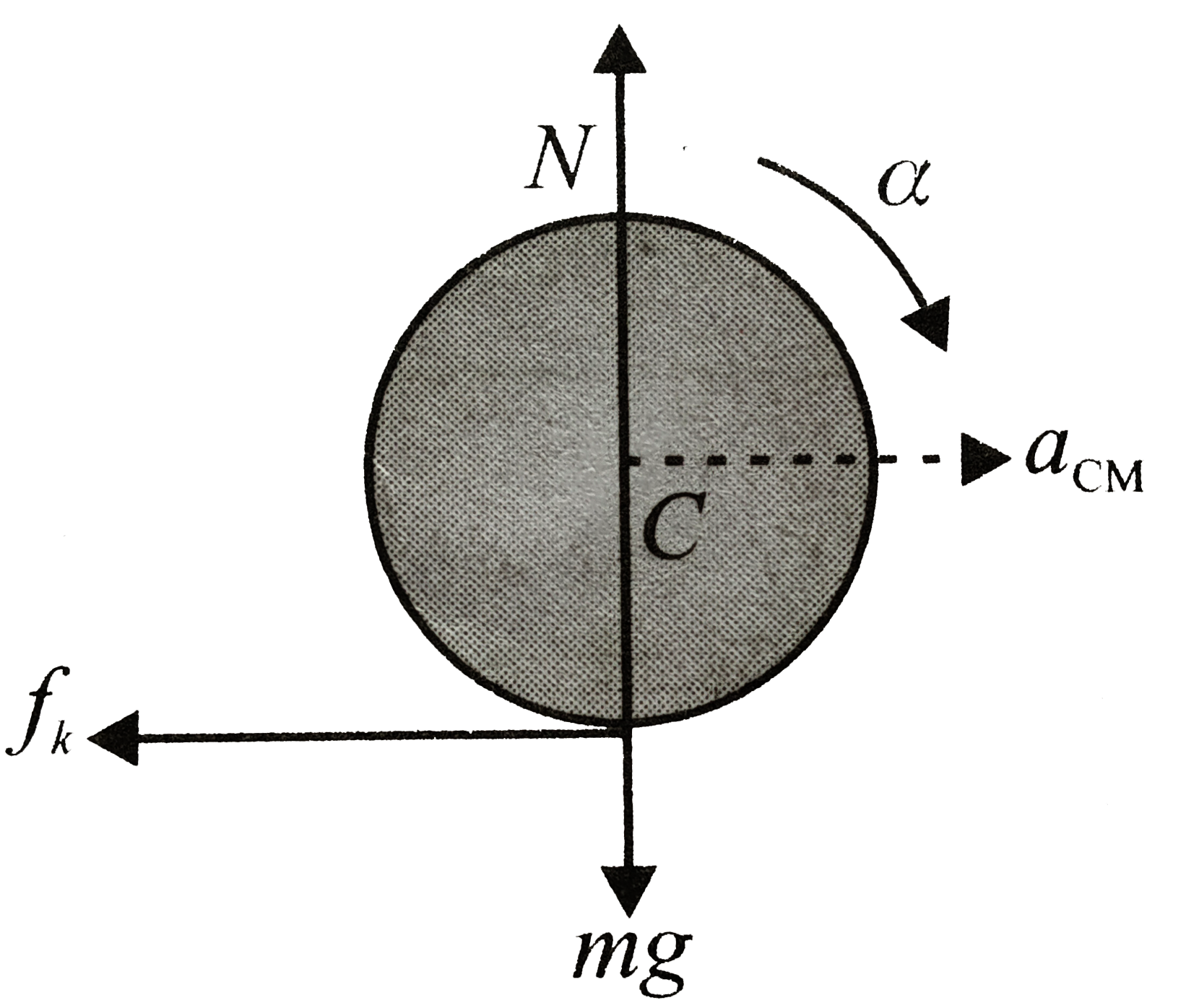
Method 1: Force/Torque Method: The forces acting on the ball are as shown in Fig. Let the acceleration of the centre of mass be `a_(CM)` and its angular acceleration about the centre of mass axis be `alpha` as shown in the figure.
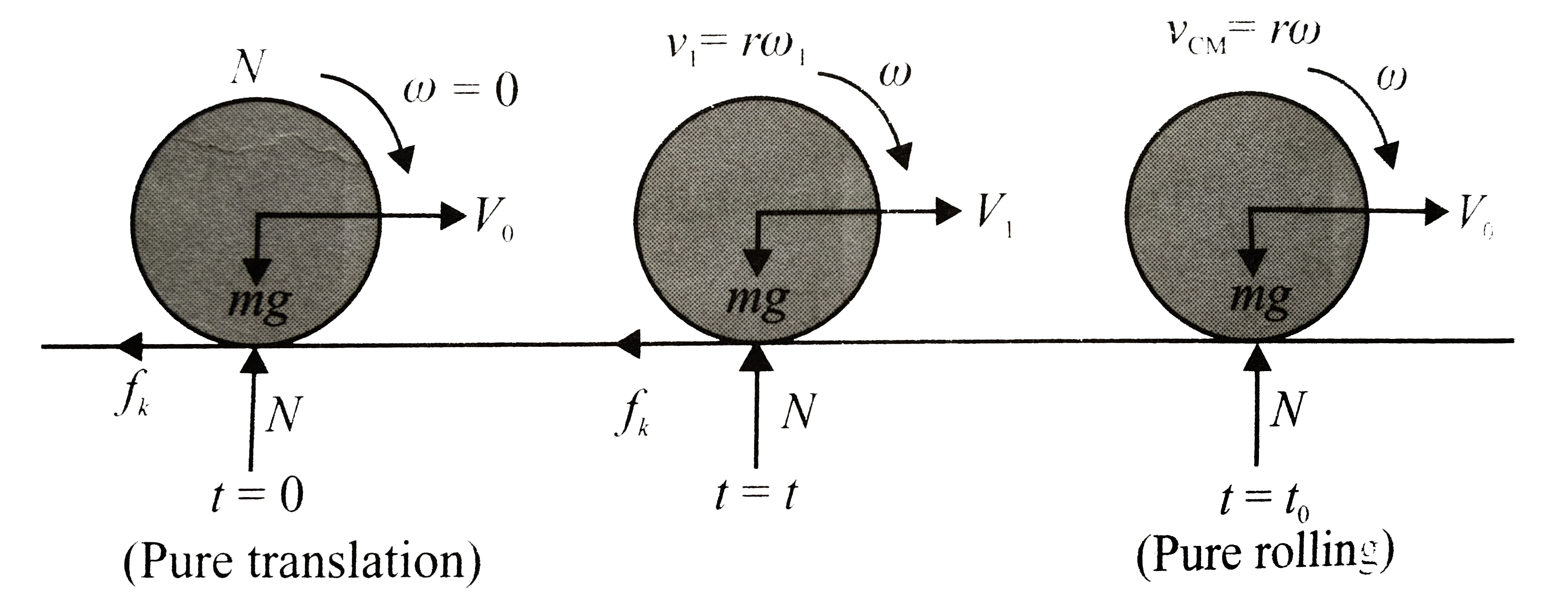
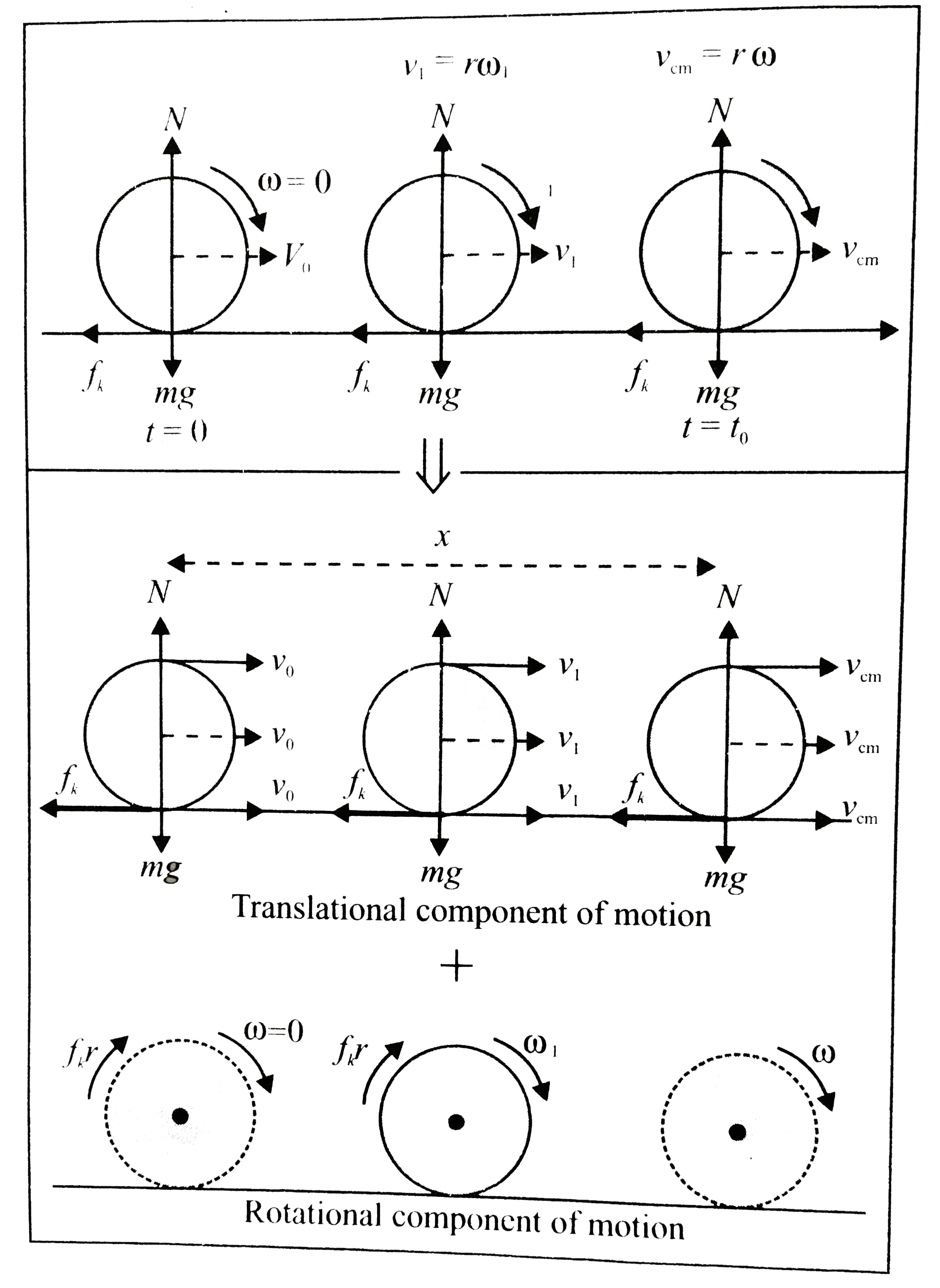
The following filgus represent the forces, accelerations and velocities of the ball in three different positions.
Force equations: `N-mg=0`(in the vertical direction)
`-f_(k)=ma_(CM)` ( in the horizontal direction)
`implies a_(CM)=-(f_(k))/m`...........i
And from `tau_(CM)=I_(CM)alpha`
`implies f_(k)r(2/5mr^(2))alpha`
`implies alpha((f_(k)r)/(2/5mr^(2)))`..........ii
Let the velocity of the centre of mass be `v_(CM)` and angular velocity about the centre of mass axis be `omega` when rolling starts.
`v_(CM)+v_(0)+((-f_(k))/m)t` (using `v=u+at`)...........iii
and `omega=0+((f_(k)r)/(2/5mr^(2)))t(omega=omega_(0)+at)`............iv
also `v_(CM)=romega`
Solving eqn iii, iv, and v for `v_(CM),` we get
`v_(CM)=5/7v_(0)`
Method 2: Work Energy Theorem
Apply the work energy theorem for the translation and rotational components of the motion separately.
`sumW_("force")=/_\K_("translational")`
`sumW_("torque")=/_\K_("rotational")`
Mathematically `W_(f_(k))+W_(N)+W_(mg)=(K_(2)-K_(2))_("translational")`
`implies -f_(k)x+0+0=1/2mv^(2)-1/2mv_(0)^(2)`
`=-f_(k)(v_(av)t)=1/2(v^(2)-v_(0)^(2)) [:'x=v_(av)t]`
`implies-f_k((v+v_(0))/2)t=1/2m(v-v_(0))(v+v_(0))` ............i
in case of constant acceleration only `v-(av)=(v_(i)+v_(f))/2`
And for the rotational component of motion
`f_(k)rtheta=1/2I_(CM)omega^(2)-0`
`rarrf_(k)r(omega_(av)t)=1/2I_(CM) omega^(2)`
`implies f_(k)r((0+omega)/2)t=1/2xx2/5mr^(2)xxomega^(2)`
[In case of constant angular acceleration `omega_(av)=(omega_(i)+omega_(f))/2`]
`implies f_(k)r omega/2t=1/2xx2/5mr^(2)omega^(2)` ..............ii
From eqn i and ii we get
`(-f_(k)(v+v_(0))/2t)/(f_(k)romega/2t)=(1/2m(v+v_(0))(v-v_(0)))/(1/2xx2/5mr^(2)omega^(2))`
`implies 1=(v-v_(0))/(2/5omegar)`
But `romega=v, `
`-1=(v-v_(0))/(2/5omegar)`
`implies -2/5v=v-v_(0)`
`implies v_(0)=v+2/5v=7/5v`
`implies v=5/7v_(0)`
Method 3: By conservation of Angular Moentum
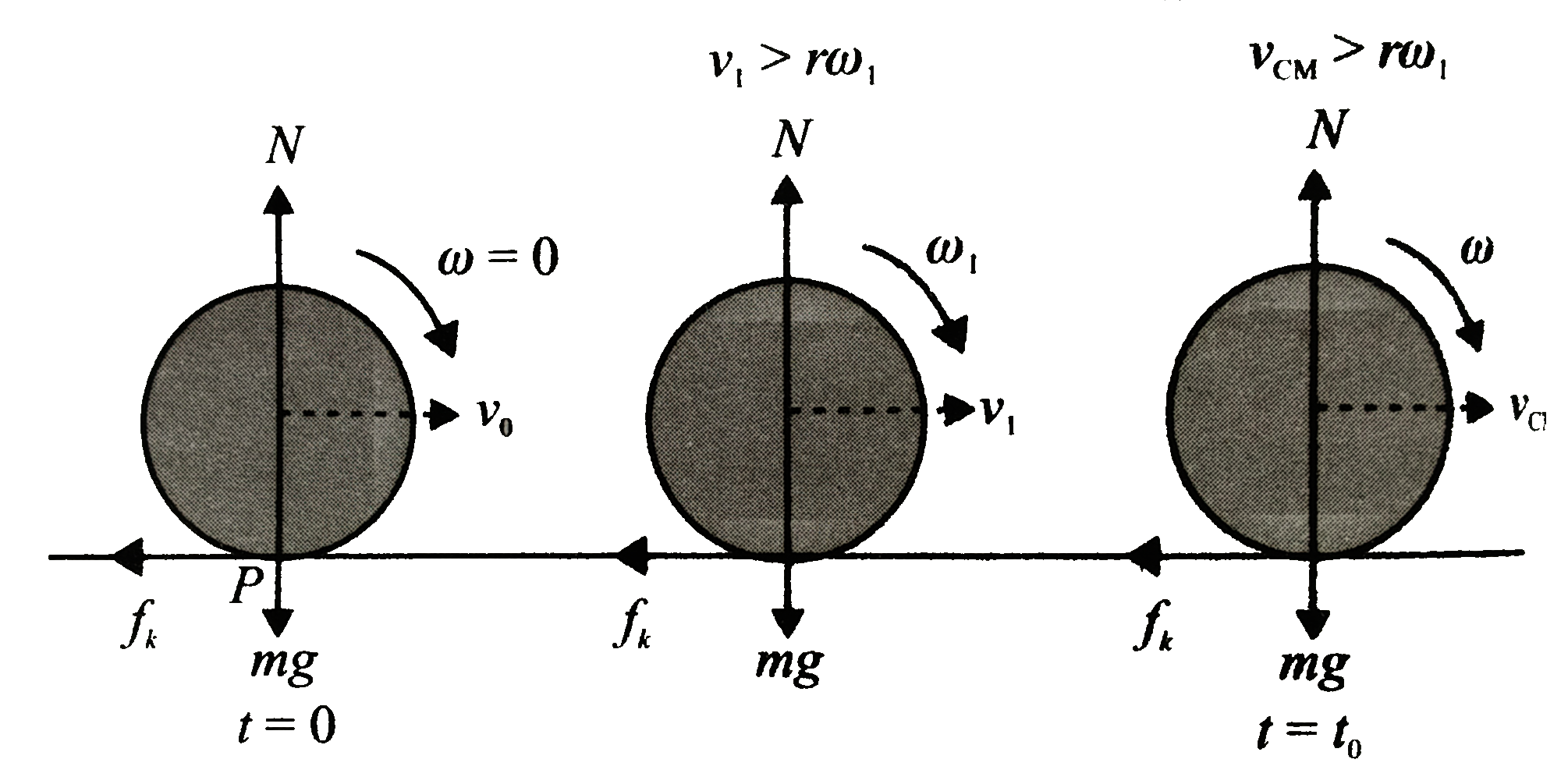
If `vectau=0 (vecdL)/(dt)=0, L=` constant
The torque acting on the ball for all its position, about point `P` (a point on the ground as shown in figure. is zero. So the anguar momentum of the ball about poitn `P` will remain constant.
`implies mv_(0)r=I_(CM)omega+mvr`
`implies mv_(0)r=2/5mr^(2)(v/r)+mvr(omega=v/r)`
`implies v_(0)=2/5v+v`
`implies v=5/7v_(0)`