Two plates `1` and `2` move with velocities `-v ` and `2v` respectively. If the sphere does not slide relative to the plates, assuming the masses of each body as `m`, find the kinetic energy of the system (plates+sphere).

Explanation

Top point of sphere in having velocity `v(larr)` and bottom point in moving with `2v(rarr)`
We can find position of `IRC`
`y/v=(2R-y)/(2v)=y=2/3R`

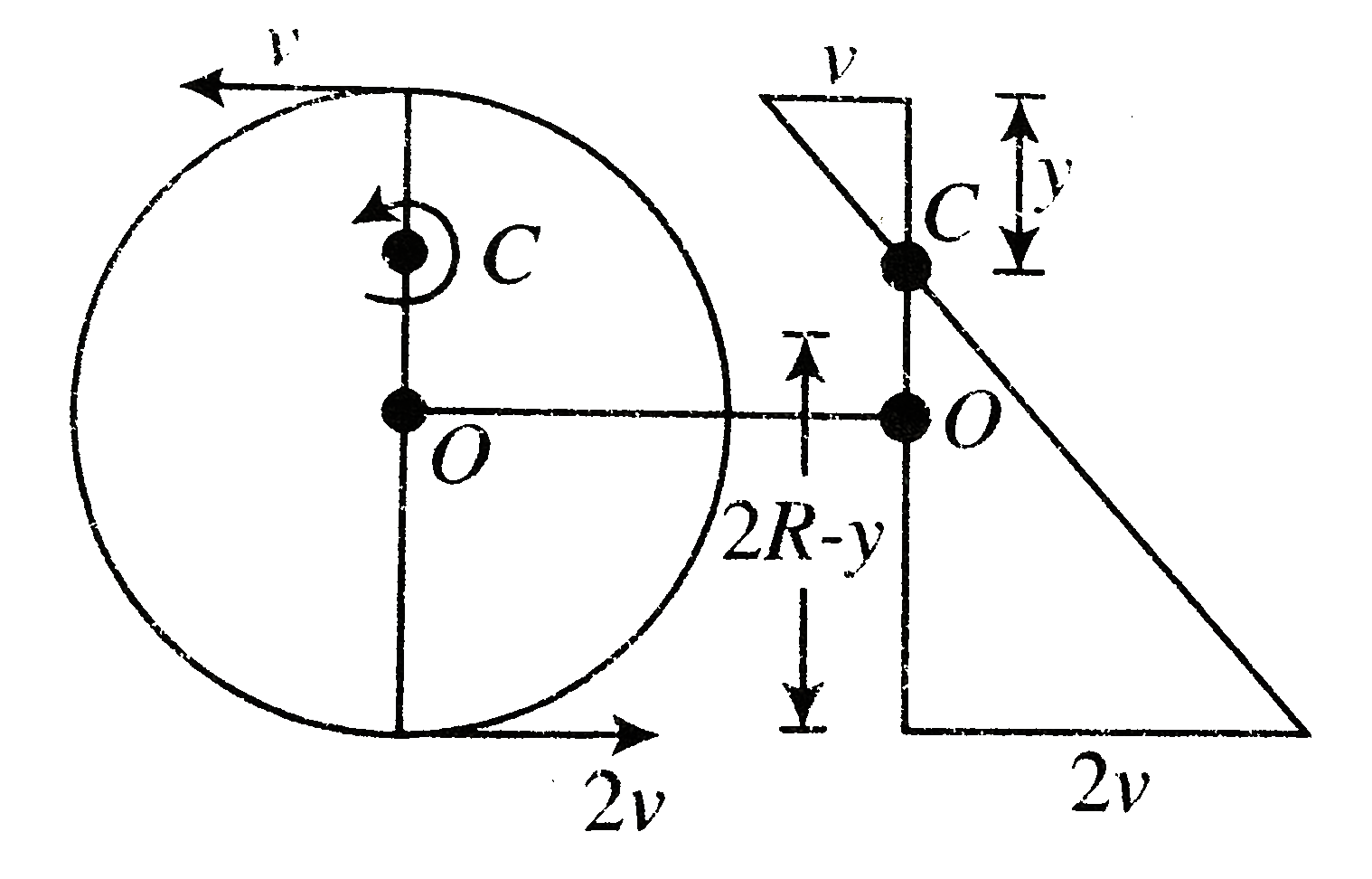
Hence we can assure the sphere will have pure rotation about `C (ICR)`
Hence the motion sphere can be considered as pure rotation about `C`.
The angular velocityi of shere `omega=v/y=(3v)/(2R)`
The kinetic energy of sphere `k_("rotation")=1/2I_(C)omega^(2)`
`implies k_("rotatioal")=1/2[2/5mR^(2)+m(OC)^(2)]omega^(2)`
`OC=R-2/3R=R/3`
`K_("rotational")=1/2(23/45mR^(2))omega^(2)=23/90momega^(2)R^(2)`
`=23/90m((3v)/(2R))^(2)R^(2)=23/40mv^(2)`
Hence total kinetic energy
`K_("total")=1/2mv^(2)+1/2m(2v)^(2)+23/40mv^(2)=123/40mv^(2)`