A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance `h` above the centre line as shown in figure. The ball leaves the cue with a speed `v_(0)` and because of its backward slipping eventually acquires a final
speed `(9)/(7)v_(0)` show that `h=(4)/(5)R`
Where `R` is the radius of the ball.

Explanation

Let `v_(0)` be the linear velocity and `omega_(0)` be the angular velocity imparted.
Linear impulse `=J=mv_(0)`

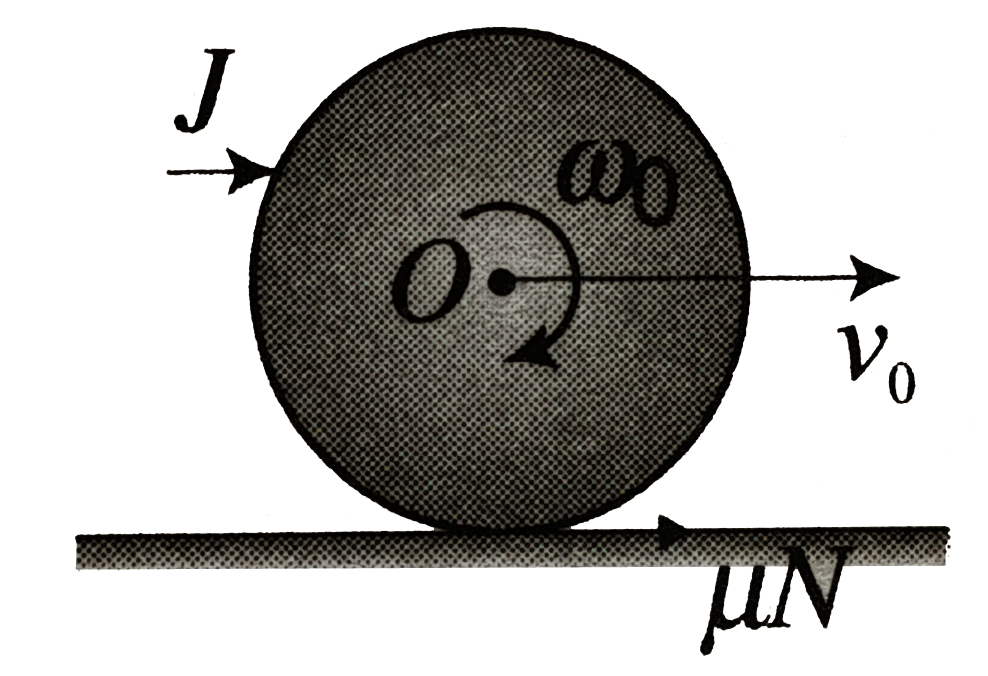
Angular impulse `=J.R=Iomega_(0)`
`impliesh=((2/5mR^(2))omega_(0))/(mv_(0))`
`implies v_(0)=(2R^(2)omega_(0))/(5h)` ..........i
As the linear velocity increases to `9//7 v_(0)`, friction must be in forwrd directiion and hence it opposes angular motion.
For lilnear motion. Friction `(mumg)` increases the velocity. Hecne, `mug=mas`
`impliesa=mug`
Let `t` be the time when rolling starts.
For rotation: Friction torque `(mumgR)` opposes rotation and hence decreases `omega`.
`alpha-(mumgR)/I`
`implies omega-omega_(0)-(mumgR)/((2/5mR^(2)))t`
After time `t, V=9/7v_(0)=Romega`
Combining all the equations, we get
`9/7v_(0)-v_(0)=-(9v_(0))/(7R)-omega_(0)(2R)/5` (eliminating `mugt`)
Substituting for `v_(0)` from eqn i we get
`2/7(2/5(R^(2)omega_(0))/h)=(omega_(0)-9/7(2Romega_(0))/(5h))(2R)/5impliesh=(4R)/5`