Let us push the wedge with a force `F` such that it moves with an acceleration a, as shown in figure. Now we can impose a pseudo force ma acting on the cylinder to write the force equation relative to the accelerating frame (wedge).
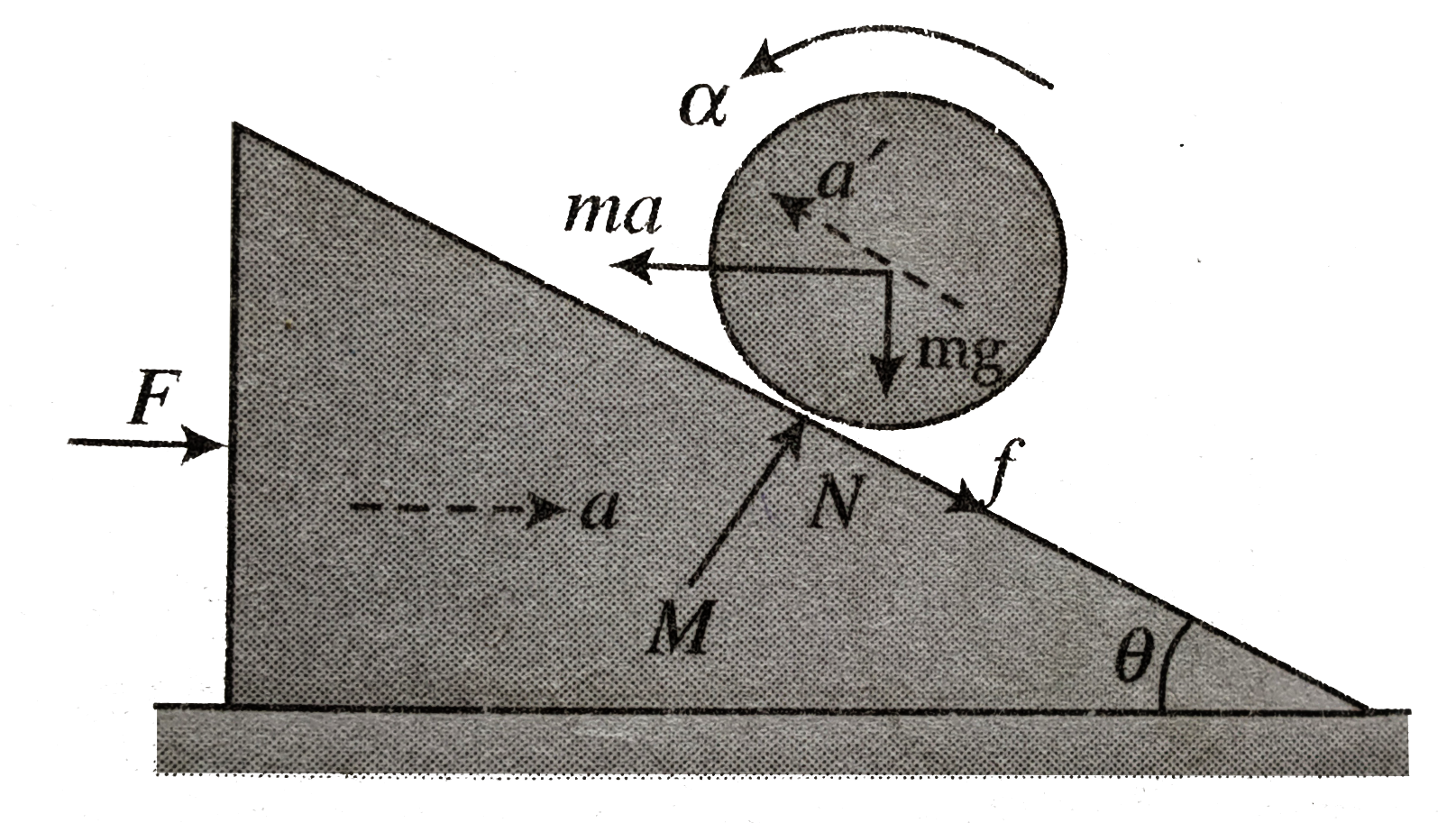
Let us assume that the cylinder rolls up with acceleration `ula'` relative to the wege. Hence, the friction of will point down the incline of the wedge.
Force equation , For `m`
`macostheta-mgsintheta-f=ma'`............i
For `m:mgcostheta+masintheta=N`..........ii
Torque equation
For `m: fr=mk^(2)alpha` .............iii
Equation of rolling of `m: a'=ralpha` ...........iv
Law of static friction : `flemuN` .............v
Eliminating `alpha` eqn iii by substituting `a'=ralpha` from eq iv we have `f=(mk^(2))/(r^(2))a'`
Substituting `a'=("fr"^(2))/(mk^(2))` in eqn i we have
`f=(macostheta-mgsintheta)/((1+(r^(2))/(k^(2))))`
Now substituting `f` from the above equation and `N` from eq ii in eq v we have
`muge(acostheta-gsintheta)/((1+(r^(2))/(k^(2)))(asintheta+gcostheta))`