A rod AB of mass `M` and length L is lying on a horizontal frictionless surface. A particle of mass `m` travelling along the surface hits the end A of the rod with a velocity `v_(0)` in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio `m//M`
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time `piL//3v_(0)` after the collision.
A rod AB of mass `M` and length L is lying on a horizontal frictionless surface. A particle of mass `m` travelling along the surface hits the end A of the rod with a velocity `v_(0)` in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio `m//M`
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time `piL//3v_(0)` after the collision.
(a). Find the ratio `m//M`
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time `piL//3v_(0)` after the collision.
Text Solution
Verified by Experts
a. If we take rod and particle as a system, the impulse between them will be internal. We can conserve the linear momentum of rod `+` particle's system. Let `V` and `omega` be the velocity and angular velocity of the `CM` just after collision.
Using conservation of linear momentum, we have
`mv_(0)=0+Mv_(c)`..........i
Here is this case we can conserve angular momentum about any point on the rod.
And by coservation of angular momentum about the entire of mass of the rod, we get
`mv_(0)L/2=lomega` or `mv_(0)L/2=((ML^(2))/12)omega`...........ii
Form eqn i and ii `v_(c)=(mv_(0))/M` and `omega= (6mv_(0))/(ML)`
We can apply conservation of anngular momentum about point of collision.
`vecL_("initial")=vecL_("final")`
`O=I_(0)omega(-hatk)+Mv_(0)l/2(hatk)`
`(ML^(2))12 omega= (Mv_(c)L)/2` .............iii
which gives `omegaL=6v_(c)`
Solving eqn i and iii we get the same results.
Since collisiion is completely elastic, therefore `KE` before collision is equa to `KE` after collision
or `1/2mv_(0)^(2)+0=1/2mv_(c)^(2)+1/2omega^(2)`
or `1/2mv_(0)^(2)=1/2M((mv_(0))/M)^(2)+1/2((6mv_(0))/(ML))^(2)`
Which gives `m/M=1/4` and `v_(c)=(v_(0))/4`
Alternative method: We can apply coefficient of restitution equation at the positioinof point of collision, we have
`e=((v_(2)-v_(1))/(u_(1)-u_(2)))`
Here `u_(1),u_(2),v_(1)` and `v_(2)` are the velocities of particles and point on the rod at collision point.
`u_(1)=v_(0), u_(2)=0`
`v_(1)=0` and `v_(2)=v_(c)+(omegal)/2`
As collision in elastic `e=1`
Substituting the values in restitution equation we get
`I=((v_(c)+omegaL)/2)-0)/(v_(0)-0)impliesv_(0)=((mv_(0))/M)+((6mv_(0))/(ML))L/2`
Which gives `m/M=1/4`
b. Velocity of point `P` immediately after collisionn is zero, let if be at a distance `y` and from `CM`
`:. v_(c)-omegay=0` or `(mv_(0))/M-((6mv_(0))/(ML))y=0`
which gives `y=L/6`
`:. AP=L/2+L/6=(2L)/3`
c. Angle rotated by the rod at time `(piL)/(3v_(0))`
`theta=omegat=((6mv_(0))/(ML))xx(piL)/(3v_(0))=pi/2`
The rod turns through `pi/2` in this interval of time. the velocity of point `P` in `y`-direction will be
`v_(y)=omega=((6mv_(0))/M)xxL/6=(v_(0))/4`
The resultant velocity of point `P`,
`v=sqrt(v_(c)^(2)+v_(y)^(2))=sqrt(((v_(0))/4)^(2)+((v_(0))/4)^(2))implies(v_(0))/(2sqrt(2))`
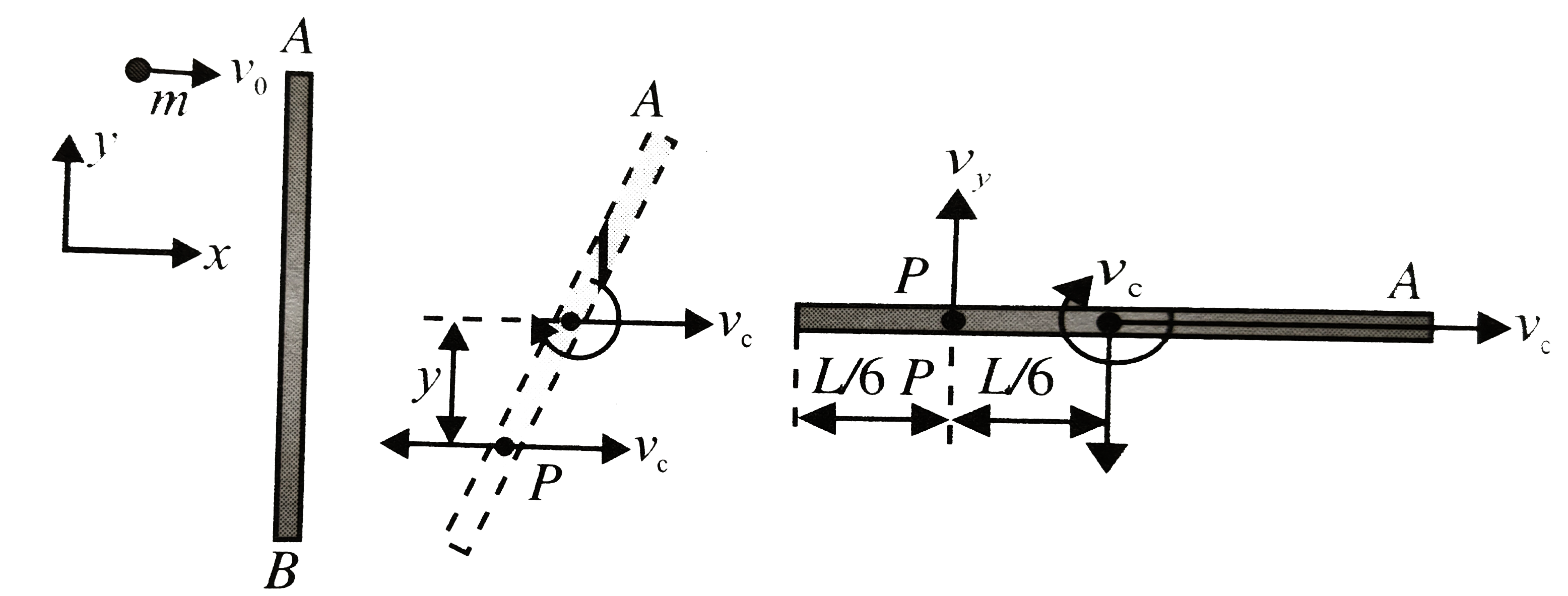
Using conservation of linear momentum, we have
`mv_(0)=0+Mv_(c)`..........i
Here is this case we can conserve angular momentum about any point on the rod.
And by coservation of angular momentum about the entire of mass of the rod, we get
`mv_(0)L/2=lomega` or `mv_(0)L/2=((ML^(2))/12)omega`...........ii
Form eqn i and ii `v_(c)=(mv_(0))/M` and `omega= (6mv_(0))/(ML)`
We can apply conservation of anngular momentum about point of collision.
`vecL_("initial")=vecL_("final")`
`O=I_(0)omega(-hatk)+Mv_(0)l/2(hatk)`
`(ML^(2))12 omega= (Mv_(c)L)/2` .............iii
which gives `omegaL=6v_(c)`
Solving eqn i and iii we get the same results.
Since collisiion is completely elastic, therefore `KE` before collision is equa to `KE` after collision
or `1/2mv_(0)^(2)+0=1/2mv_(c)^(2)+1/2omega^(2)`
or `1/2mv_(0)^(2)=1/2M((mv_(0))/M)^(2)+1/2((6mv_(0))/(ML))^(2)`
Which gives `m/M=1/4` and `v_(c)=(v_(0))/4`
Alternative method: We can apply coefficient of restitution equation at the positioinof point of collision, we have
`e=((v_(2)-v_(1))/(u_(1)-u_(2)))`
Here `u_(1),u_(2),v_(1)` and `v_(2)` are the velocities of particles and point on the rod at collision point.
`u_(1)=v_(0), u_(2)=0`
`v_(1)=0` and `v_(2)=v_(c)+(omegal)/2`
As collision in elastic `e=1`
Substituting the values in restitution equation we get
`I=((v_(c)+omegaL)/2)-0)/(v_(0)-0)impliesv_(0)=((mv_(0))/M)+((6mv_(0))/(ML))L/2`
Which gives `m/M=1/4`
b. Velocity of point `P` immediately after collisionn is zero, let if be at a distance `y` and from `CM`
`:. v_(c)-omegay=0` or `(mv_(0))/M-((6mv_(0))/(ML))y=0`
which gives `y=L/6`
`:. AP=L/2+L/6=(2L)/3`
c. Angle rotated by the rod at time `(piL)/(3v_(0))`
`theta=omegat=((6mv_(0))/(ML))xx(piL)/(3v_(0))=pi/2`
The rod turns through `pi/2` in this interval of time. the velocity of point `P` in `y`-direction will be
`v_(y)=omega=((6mv_(0))/M)xxL/6=(v_(0))/4`
The resultant velocity of point `P`,
`v=sqrt(v_(c)^(2)+v_(y)^(2))=sqrt(((v_(0))/4)^(2)+((v_(0))/4)^(2))implies(v_(0))/(2sqrt(2))`
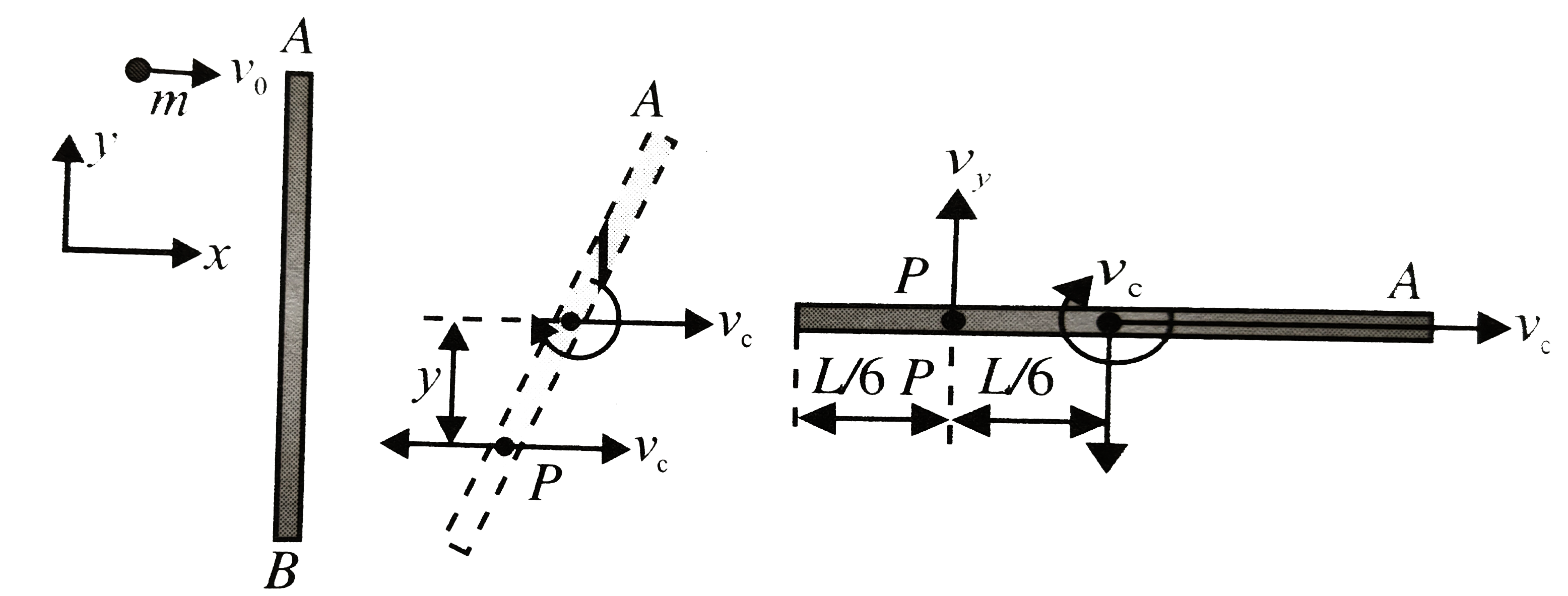
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v_(0) in a direction perpendicular to AB . The collision is completely elastic. After the collision the particle comes to rest. Find the ration m//M .
A rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with a velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses ((m)/(M))" is "(1)/(x) . The value of 'x' will be_____.
A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance (L)/(2) from COM with a velocity v_(0) in a direction perpendicular to rod and sticks to it. Angular velocity of rod just after collision is
A rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37^@ with the rod. The collision is elastic. After collision,
A rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
A rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v_(0) , perpendicular to the rod, collides elastically with the free end of the rod. Find: a. the angular velocity of the rod after collision. b. the impulse applied by the pivot on the rod during collision. (Take M//m = 2 )