Home
Class 11
PHYSICS
A smooth hemispherical bowl 30 cm diame...

A smooth hemispherical bowl ` 30 cm` diameter potates with a constatn angular velocity `omega`, about its vertical axis of symmetry. A particle at (P) of weighing ` 5 kg`, is onserved to remantn at rest telative to the bowal at a height ` 10 cm` above teh base, Fig. 1 (CF) . 34. The magnitude fo speed of rotation of the bowl is
.

A

` 15 rad//s`

B

` 23 rad//s`

C

` 14 rad//s`

D

` 16 rad//s`

Text Solution

Verified by Experts

The correct Answer is:
C
Let` R` be the force exerted by the bowl in the particle. It will be as a reactional force (R ). Various forces acting on particle at (P) will be (i) weight
Mg (downwards ) (ii) ` R` (Normal reaction ) along (PO).
.
Resolving (R ) into tis two rectangular components we have ` R sin theta ` acts vertically wpards and ` R cos thea ` acts horizontally along ` PQ` As horizontal component ` R cos theta ` will proved required centripetal force.
` :. ` R cos theta = ma_c`
[a_c rarr centripetal accleration]`
` R cos theta mr omega^2 ` or ` omega= sqrt (R cos theta)/(mr)`
` cos theta = theta r/(OP) = r/(0.15)`
[:. R sin theta = mg
R = (mg)/(sin theta)= (mg)/(OQ//OP) = ( 5 xx 9.8)/(0.05 //0 15/
(R = 15 xx 9.8 N)]`
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    PRADEEP|Exercise 4 NCERT multiple Choice|10 Videos

  • KINEMATICS

    PRADEEP|Exercise 4 NCERT Integer type|4 Videos

  • KINEMATICS

    PRADEEP|Exercise 2 NCERT multiple|15 Videos

  • GRAVIATION

    PRADEEP|Exercise Assertion-Reason Type Questions|19 Videos

  • LAWS OF MOTION

    PRADEEP|Exercise Assertion- Reason Type Questions|17 Videos

Similar Questions

Explore conceptually related problems

A smooth hemispherical bowl 30 cm diameter, rotates with a constant angular velocity omega , about its vertical axis of symmetry Fig. 2 (APC) . 2 (a) . A particle at (P) of weighing 5 kg is observed to remain at rest relative to the bowl at a height 10 cm above the base. Find the magnitude of the force exerted by the bowl on the particle and speed of rotation of the bowl. .

A rough horizontal plate rotates with a constant angular velocity w about its vertical axis. A particle of mass m lies on the plate at a distance (5a)/(4) from the axes. If the coefficient of friction is (1)/(3) and the particle remains at rest relative to the plane, show that w le sqrt((4g)/(15a)) . The particle is now connected to axis by a horizontal elastic string, of natural length a and modulus 3 mg. If the particle remains at rest relative to the plate and at a distance (5a)/(4) , show that the greatest possible angular velocity is sqrt((13)/(15).(g)/(a)) and find the least possible velocity.

A horizontal disc rotates with a constant angular velocity omega=6.0rad//s about a vertical axis passing through its centre. A diameter of the disc with a velocity v^'=50cm//s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r=30cm from the rotation axis.

A horizontal smooth rod AB rotates with a constant angular velocity omega=2.00rad//s about a vertical axis passing through its end A. A freely sliding sleeve of mass m=0.50g moves along the rod from the point A with the initial velocity v_0=1.00m//s . Find the Coriolis force acting on the sleeve (in the reference frame fixed to rotating rod) at the moment when the sleeve is located at the distance r=50cm from the rotation axis.

A uniform solid cone of mass m, base radius ‘R’ and height 2R, has a smooth groove along its slant height as shown in figure. The cone is rotating with angular speed omega , about the axis of symmetry. If a particle of mass ‘m’ is released from apex of cone, to slide along the groove, then angular speed of cone when particle reaches to the base of cone is

A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega . where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk) . A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The distance r of the block at time is

A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega . where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk) . A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The net reaction of the disc on the block is

A particle is placed inside a hemispherical bowl which rotates about its vertical axis with constant angular speed omega . It is just prevented from sliding down when the line joining it to the centre of the hemisphere is 45^(@) with the vertical. The radius of the bowl is 10 sqrt(2) m. The coefficient of friction between the particle and the bowl is 0.5 and g = 10 ms^(-2) . Find the magnitude of omega .

A hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity omega . A particle on the frictionless inner surface of the bowl is also rotating with the same omega . The particle is a height h from the bottom of the bowl. (i) Obtain the relation between h and omega _________ (ii) Find minimum value of omega needed, in order to have a non-zero value of h _____________ .

PRADEEP-KINEMATICS-3 NCERT multiple
  1. A particle is moving in a circular path with a constant speed. If thet...

    Text Solution

    |

  2. A particle moves along a circle if radius (20 //pi) m with constant ta...

    Text Solution

    |

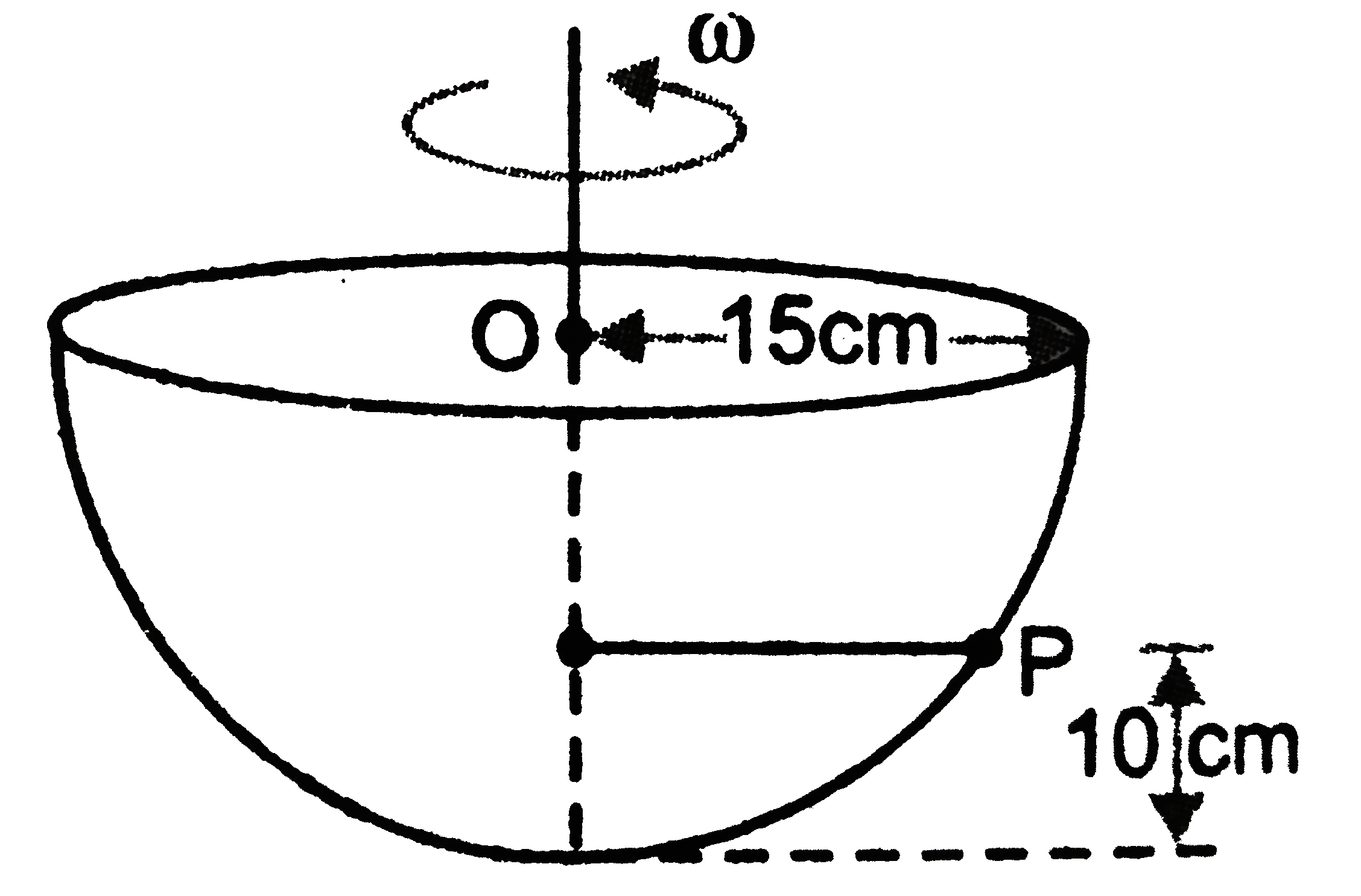
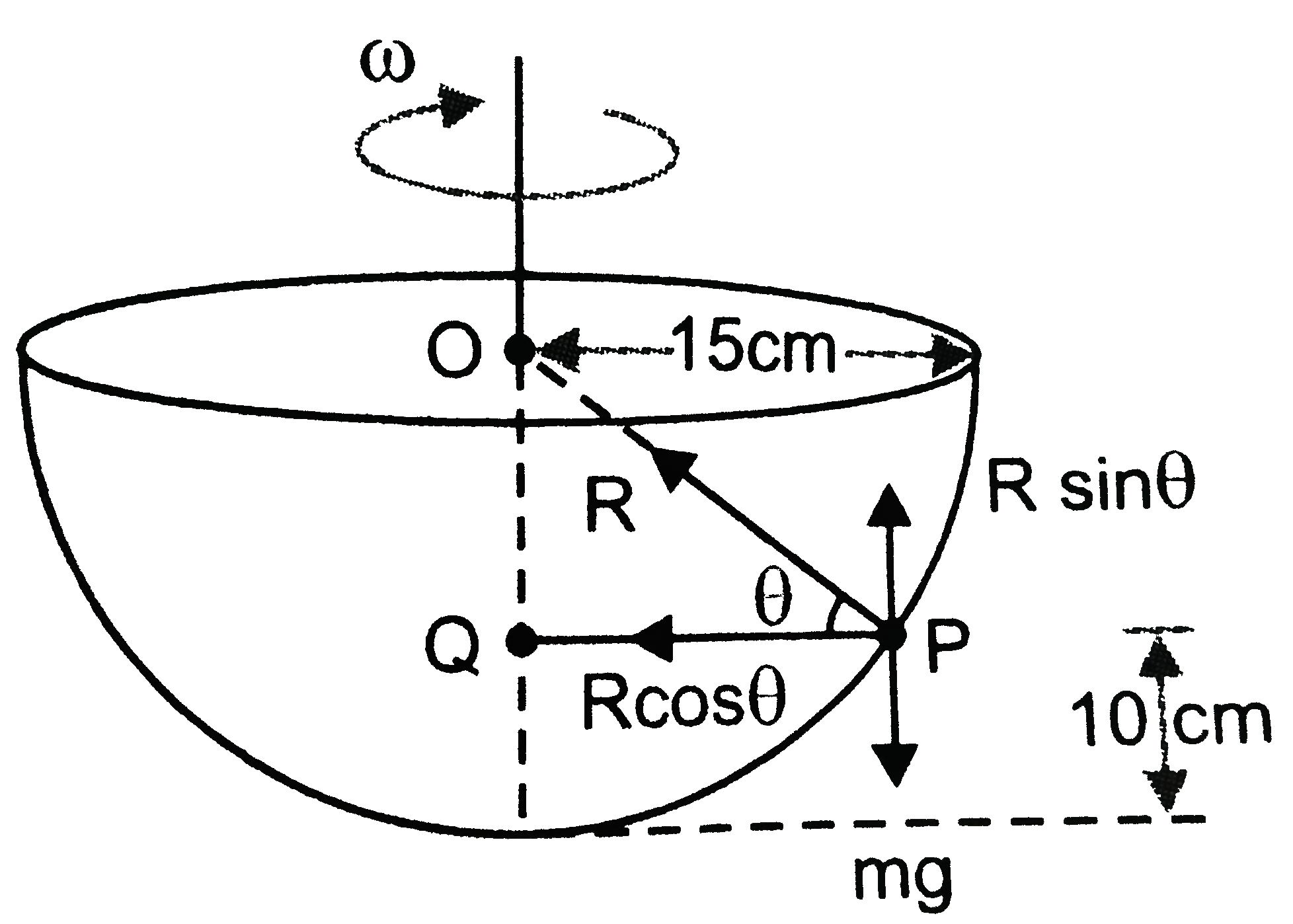
  3. A smooth hemispherical bowl 30 cm diameter potates with a constatn an...

    Text Solution

    |

  4. A sphere is rolling without slipping on a fixed horizontal plane surfa...

    Text Solution

    |

  5. A point p moves in counter - clockwise direction on a circular path a...

    Text Solution

    |

  6. For a particle in uniform circular motion , the acceleration vec(a) a...

    Text Solution

    |

  7. Consider a disc rotating in the horizontal plane with a constant angul...

    Text Solution

    |

  8. Two identical discs of same radius R are rotating about their axes in ...

    Text Solution

    |

  9. Which of the following statemeents are true for motion with uniform ve...

    Text Solution

    |

  10. An object while moving may not have .

    Text Solution

    |

  11. A particle moves along the X-axis as x=u(t-2s)=at(t-2)^2.

    Text Solution

    |

  12. Choose the correct statement for a particle going on a straight line.

    Text Solution

    |

  13. Which of the following is not an example of projectile motion.

    Text Solution

    |

  14. Which of the following doesnt represent the relation of angular projec...

    Text Solution

    |

  15. A particle is moving on a straight line path with constant accleration...

    Text Solution

    |

  16. A particle is forced to meove on a straight line path. It returns to t...

    Text Solution

    |

  17. A ball is thrown vertically upwards from the ground. If T1 and T2 are ...

    Text Solution

    |

  18. Acceleration of a particle which is at rest at x=0 is vec a = (4 -2 ...

    Text Solution

    |

  19. The motion of a body is given by the equation dv//dt=6-3v, where v is ...

    Text Solution

    |

  20. A particl leaves the orgin with an lintial veloity vec u = (3 hat I )...

    Text Solution

    |