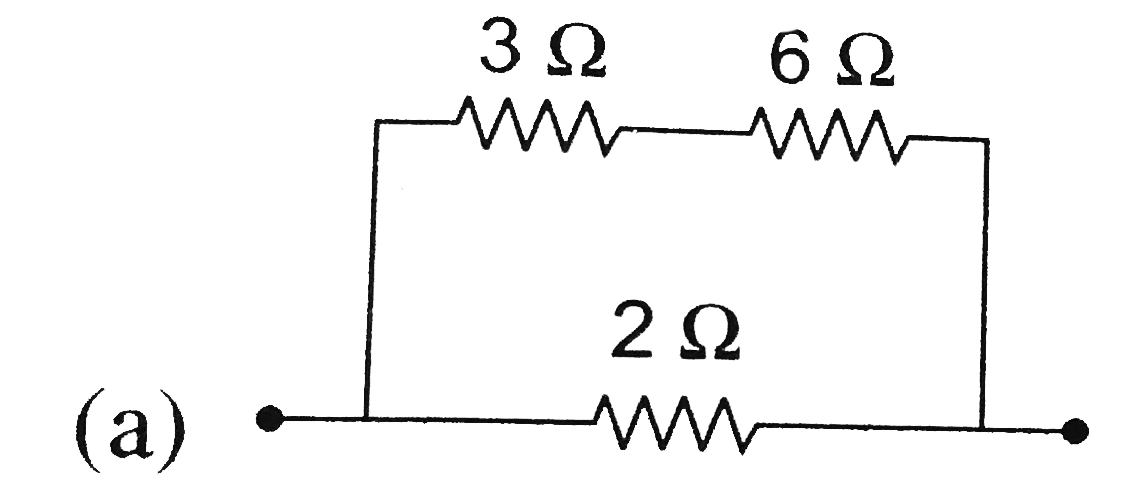
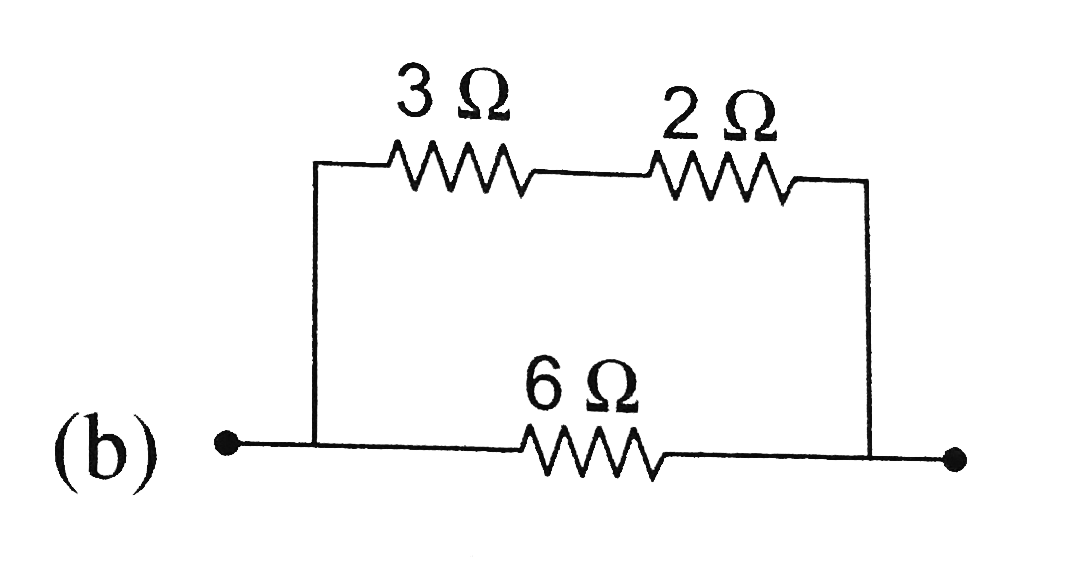
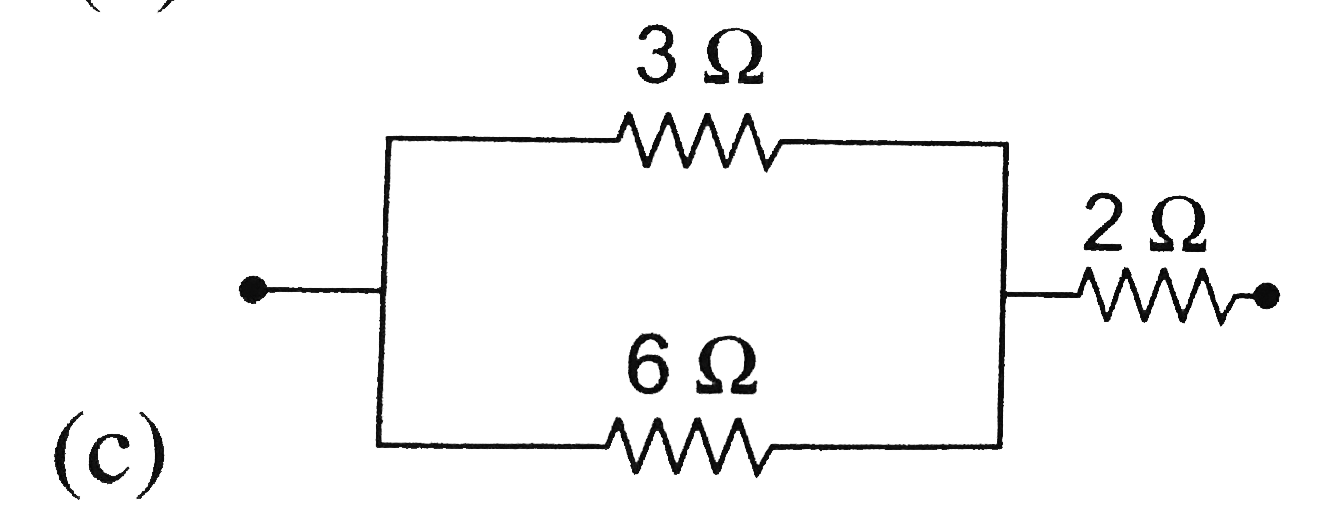
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
CURRENT ELECTRICITY
A2Z|Exercise Kircoff'S Laws And Simple Circuits|64 VideosCURRENT ELECTRICITY
A2Z|Exercise R-C Circuits|17 VideosCURRENT ELECTRICITY
A2Z|Exercise Section D - Chapter End Test|29 VideosATOMIC PHYSICS
A2Z|Exercise Section D - Chapter End Test|30 VideosDUAL NATURE OF RADIATION AND MATTER
A2Z|Exercise Section D - Chapter End Test|30 Videos
Similar Questions
Explore conceptually related problems
A2Z-CURRENT ELECTRICITY-Combination And Resistivity
- A prism is made of wire mesh with each side having equal resistance R....
Text Solution
|
- Find the equivalent resistance across AB :
Text Solution
|
- If you are provided three resistance 2 Omega, 3 Omega and 6 Omega. How...
Text Solution
|
- In the circuit given E = 6.0 V, R(1) = 100 ohms, R(2) = R(3) = 50 ohms...
Text Solution
|
- In the diagram resistance across terminals A and B is
Text Solution
|
- The effecitve resistance between A and B of the shown network, where r...
Text Solution
|
- In the arrangement shown, the magnitude of each resistance is 2 Omega....
Text Solution
|
- Seven resistances are connected as shown in the figure. The equivalent...
Text Solution
|
- The equivalent resistance between the point A and B is
Text Solution
|
- Four resistances 10 Omega, 5 Omega, 7 Omega and 3 Omega are connected ...
Text Solution
|
- Thirteen resistances each of resistance R ohm are connected in the cir...
Text Solution
|
- The resistance of all the wires between any two adjacent dots is R. Th...
Text Solution
|
- An infinite sequence of resistance is shown in the figure. The resulta...
Text Solution
|
- The equivalent resistance of the following infinite network of resista...
Text Solution
|
- In the figure, the value of resistors to be connected between C and D ...
Text Solution
|
- What is the equivalent resistance between the point A and B of the net...
Text Solution
|
- The effective resistance between points P and Q of the electrical ci...
Text Solution
|
- The equivalent resistance between the point P and Q in the network giv...
Text Solution
|
- Kirchhoff's first law i.e., sum I = 0 at a junction is based on the la...
Text Solution
|
- Kirchoff's second law is based on the law of conservation of
Text Solution
|