(i) Consider a thin lens placed between a source (S) and an observer (O), Fig. Let the thickness of the lens vary as `w (b) = w_0 - (b^2)/(prop)`, where `b` is the vertical distance from the pole. `w_0` is a constant. Using Fermat's principle, i.e., the time of transit for a ray between the source and observer is an exptremum, find the condition that al paraxial rays starting from the source will converge at a point `O` on the axis. Find the focal length.
(ii) A gravitational lens may be assumed to have a varying width of the form
`w(b) = k_1 In ((k_2)/(b)) b_min lt b lt b_(max) w(b) = k_1 In ((k_2)/(b_(min))) b lt b_(min)`
Show that an observer will see an image of a point object as a ring about the center of the lens with an angular radius `beta = sqrt(((n - 1) k_1 (u)/(v))/(u + v))`.
.

Explanation

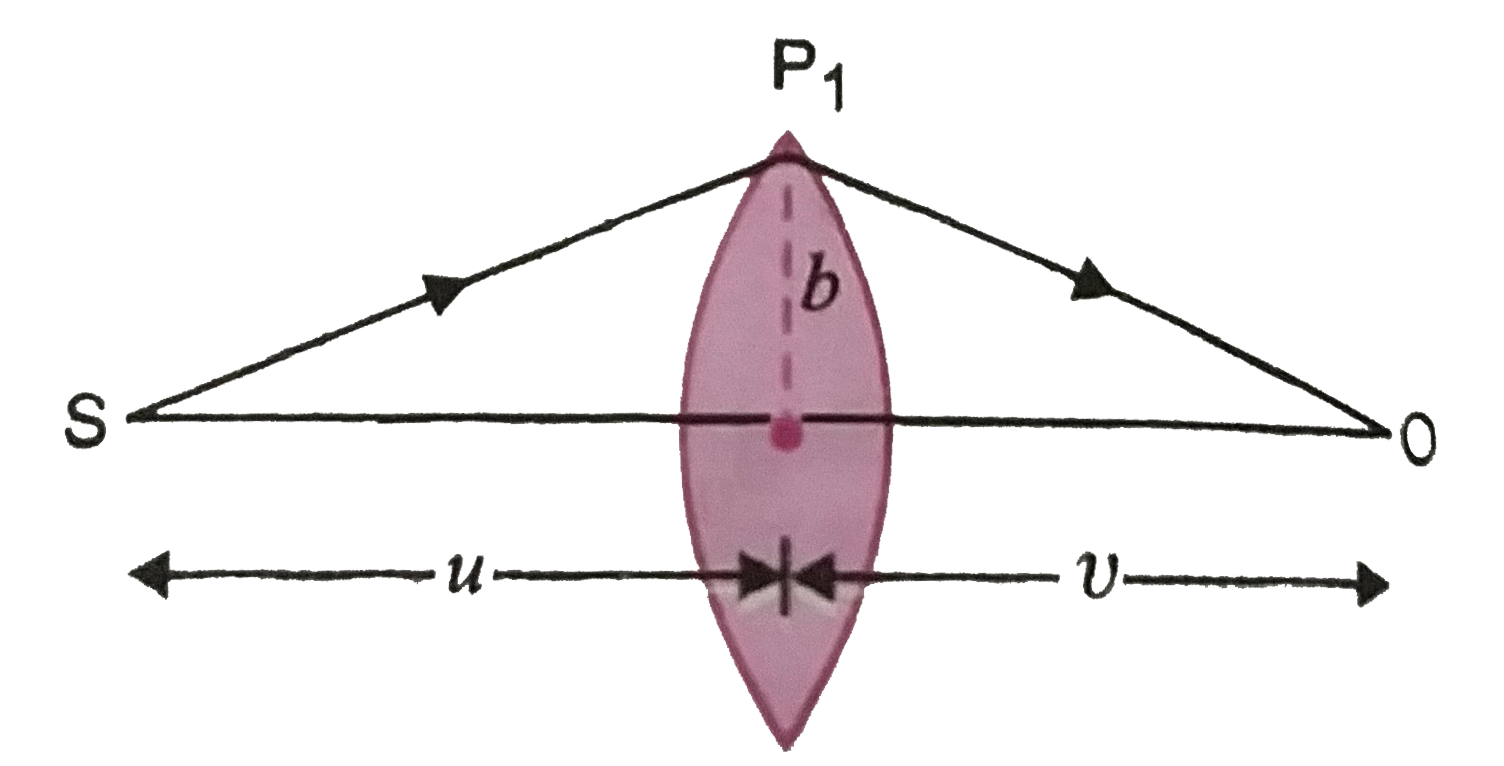
Time required by ligth to travel in air from `S to P_1` is
`t_1 = (SP_1)/( c) = (sqrt(u^2 + b^2))/( c)`
=`(u)/( c)[1 + (1)/(2) (b^2)/(u^2)]`, assuming `b lt lt u`
Similarly, time required by light to travel in air from `P_1 to O , = (v)/( c) (1 + (1)/(2) (b^2)/(v^2))`
Now, thickness of lens varies as `w(b) = w_0 - (b^2)/(prop)`...(i)
`:.` Time required to travel through the lens is `t_3 = (w(b))/(c//n) -(w(b))/( c) = ((n-1) w(b))/( c)`
Here, `n` is refractive index of the material of the lens.
Thus, the total time of travel from `S to O` is
`t = t_1 + t_2 + t_3 = (u)/(c)(1 + (b^2)/(2 u^2)) + (v)/(c) (1 + (b^2)/(2 v^2)) + ((n - 1)w(b))/( c)`
`t = (1)/( c) [u + v + (1)/(2) b^2 ((1)/(u) + (1)/(v)) + (n - 1) w(b)]`
Let us put `(1)/(u)+(1)/(v)=(1)/(D)` ...(ii)
`t = (1)/( c) [u + v + (b^2)/(2 D) +(n - 1) (w_0 - (b^2)/(prop))]`...(iii)
According to Fermat's principle, `t` = extremum. Therefore `(dt)/(db) = 0`
From (iii), `(dt)/(db) = (b)/(cD) -(2(n - 1)b)/(c prop) = 0` or `prop = 2 (n -1) D` ...(iv)
Hence, a convergent lens is formed if `prop = 2(n - 1) D`. This is independent of `b`. Hence, all paraxial rays from `S` will converge `O`.
From (ii), `(1)/(u)+(1)/(v)=(1)/(D)`. Therefore, focal length of lens `= D`
(ii) Now, for a gravitational lens, `w(b) = k_1 log_e ((k_2)/(b)) , b_(min) lt b lt b_(max)`
`w(b) = k_1 log_e ((k_2)/(b_(min))) , b lt b_(min)`
Proceeding as in the above case, from eqn. (iii)
`t = (1)/(2) [u + v + (1)/(2) (b^2)/(D) + (n -1 ) k_1 log_e((k_2)/(b))]`
`(dt)/(db) = 0 = (b)/(D) - (n -1)(k_1)/(b)`
`:. b^2 = (n - 1) k_1 D`
`b = sqrt((n - 1) k_1 D)`
Hence, all rays passing through the lens at a height `b` shall from the image.
The paths of rays would make an angle
`beta =(b)/(v) = (sqrt((n - 1) k_1 D))/(sqrt(v^2)) = sqrt(((n - 1) k_1 uv)/(v^2 (u + v)))` `(as (1)/(d)=(1)/(u)+(1)/(v))`
`beta = sqrt(((n - 1) k_1 u//v)/((u + v)))`
Hence, the observer will see an image of a point object as a ring about the centre of the lens with with an angular radius `beta`.
.