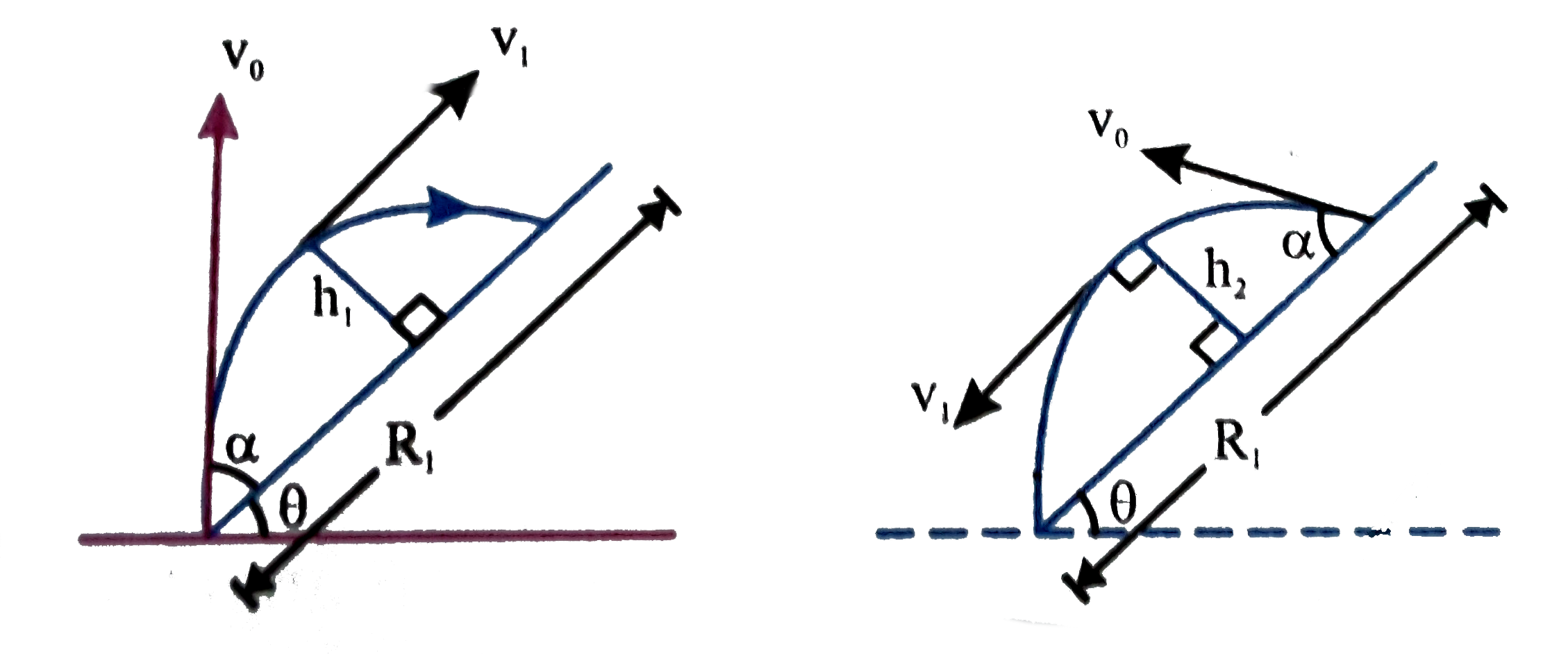
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOTION IN A PLANE
NARAYNA|Exercise Level-VI Passage answer|18 VideosMOTION IN A PLANE
NARAYNA|Exercise Level-Vi Integer|9 VideosMOTION IN A PLANE
NARAYNA|Exercise Level-Vi single answer|30 VideosMECHANICAL PROPERTIES OF SOLIDS
NARAYNA|Exercise LEVEL-II (H.W)|24 VideosMOTION IN A STRAIGHT LINE
NARAYNA|Exercise Level 2 H.W|29 Videos
Similar Questions
Explore conceptually related problems
NARAYNA-MOTION IN A PLANE-Level-Vi multiple answer
- A child in danger of drowning in a river is being carried downstream b...
Text Solution
|
- A launch plies between two points A and B on the opposite banks of a r...
Text Solution
|
- The current velocity of river grows in proportion to the distance from...
Text Solution
|
- Two swimmers A and B start swimming from different positions on the sa...
Text Solution
|
- Two frames of reference P and Q are moving relative to each other at c...
Text Solution
|
- Two swimmers start a race. One who reaches the point C first on the ot...
Text Solution
|
- Two trains A and B are moving with same speed of 100km//hr.Train A mov...
Text Solution
|
- Two shells are fired from cannon with speed u each, at angles of alpha...
Text Solution
|
- Two inclined planes OA and OB having inclination (with horizontal) 30^...
Text Solution
|
- Two balls are thrown from an inclined plane at angle of projection alp...
Text Solution
|
- An aeroplane at a constant speed releases a bomb.As the bomb drops awa...
Text Solution
|
- Two particles are projected with speed 4m//s and 3m//s simultaneously ...
Text Solution
|
- A particle moves along x-axis with constant acceleration and its x-pos...
Text Solution
|
- A railway compartments is 16 m long, 2.4 m wide and 3.2 m high. It is ...
Text Solution
|
- Two particles A and B are projected from the same point with the same ...
Text Solution
|
- Two particles are projected from the same point, with the same speed, ...
Text Solution
|