Home
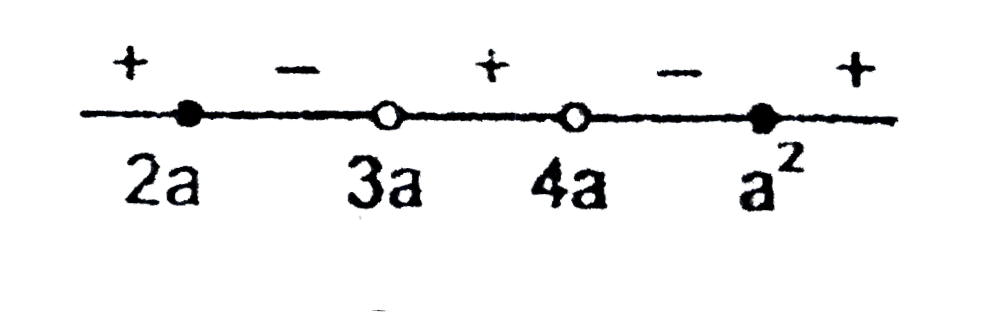
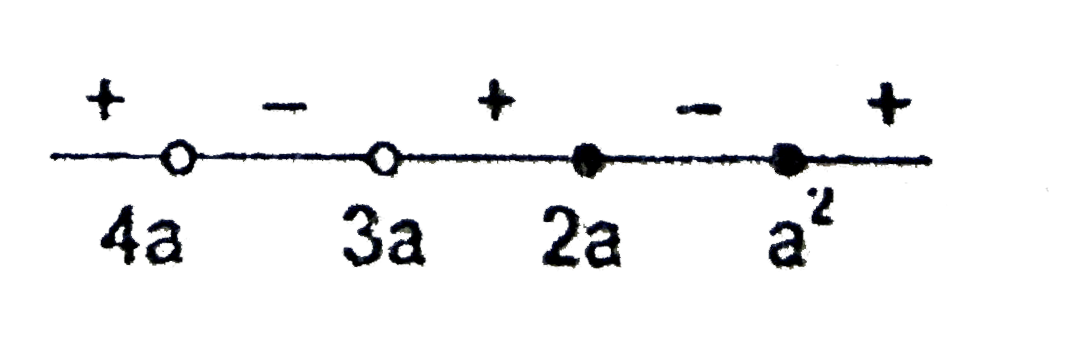Class 12
MATHS
Let 'a' be an integer. If there are 10 i...

Let `'a'` be an integer. If there are `10` inegers satisfying the `((x-a)^(2)(x-2a))/((x-3a)(x-4a))le0` then

A

`a` is prime number

B

`e^(a) lt pi^(a)`

C

`a^(2) - 2` is prime number

D

number of possible values of `a` is `2`

Text Solution

Verified by Experts

The correct Answer is:
C, D
If `a gt 0`

`x in [(2a, 3a) cup (4a, a^(2))]`
`:. (a^(2) - 4a) + (3a - 2a) = 10`
`a^(2) - 3a - 10 = 0`
`(a - 5) (a + 2) = 0 rArr a = 5`
if `a lt 0`

`x epsilon (4a, 3a) cap [2a, a^(2)]`
`:. (a^(2) - 2a + 1) + (3a - 4a - 1) = 10`
`rArr a^(2) - 3a - 10 = 0`
`(a - 5) (a + 2) = 0 rArr a = -2`
`:. a in {-2, 5}`
Promotional Banner

Topper's Solved these Questions

  • TEST PAPERS

    RESONANCE|Exercise PART - I MATHEMATICS SEC - 2|1 Videos

  • TEST PAPERS

    RESONANCE|Exercise PART - I MATHMATICS|84 Videos

  • TEST PAPERS

    RESONANCE|Exercise PART : 1MATHEMATICS SEC - 2|10 Videos

  • TEST PAPER

    RESONANCE|Exercise CHEMISTRY|37 Videos

  • TEST SERIES

    RESONANCE|Exercise MATHEMATICS|131 Videos

Similar Questions

Explore conceptually related problems

let a>2,a in N be a constant.If there are just 18 positive integers satisfying the inequality (x-a)(x-2a)(x-a^(2))<0 then which of the option is correct

Solve ((x-5)^(2)(x+2)^(3)(x-4))/((x-3)^(4))le0

Let a>2 be a constant.If there are just 18 positive integers satisfying the inequality (x-a)(x-2a)(x-a^(2))<0, then find the value of a.

Solve ((2x+3)(4-3x)^3(x-4))/((x-2)^2x^5)le0

Sum of integral value(s) of x satisfying the inequality (x^(2)-3x-10)/(x^(2)+x+1)le0 , is

The number of integers satisfying |2x-3|+|x+5| le |x-8| is

The set of values of x satisfying |(x^(2)-5x+4)/(x^(2)-4)| le 1 is

The number of solutions (x,y) where x and y are integers,satisfying 2x^(2)+3y^(2)+2x+3y=10 is