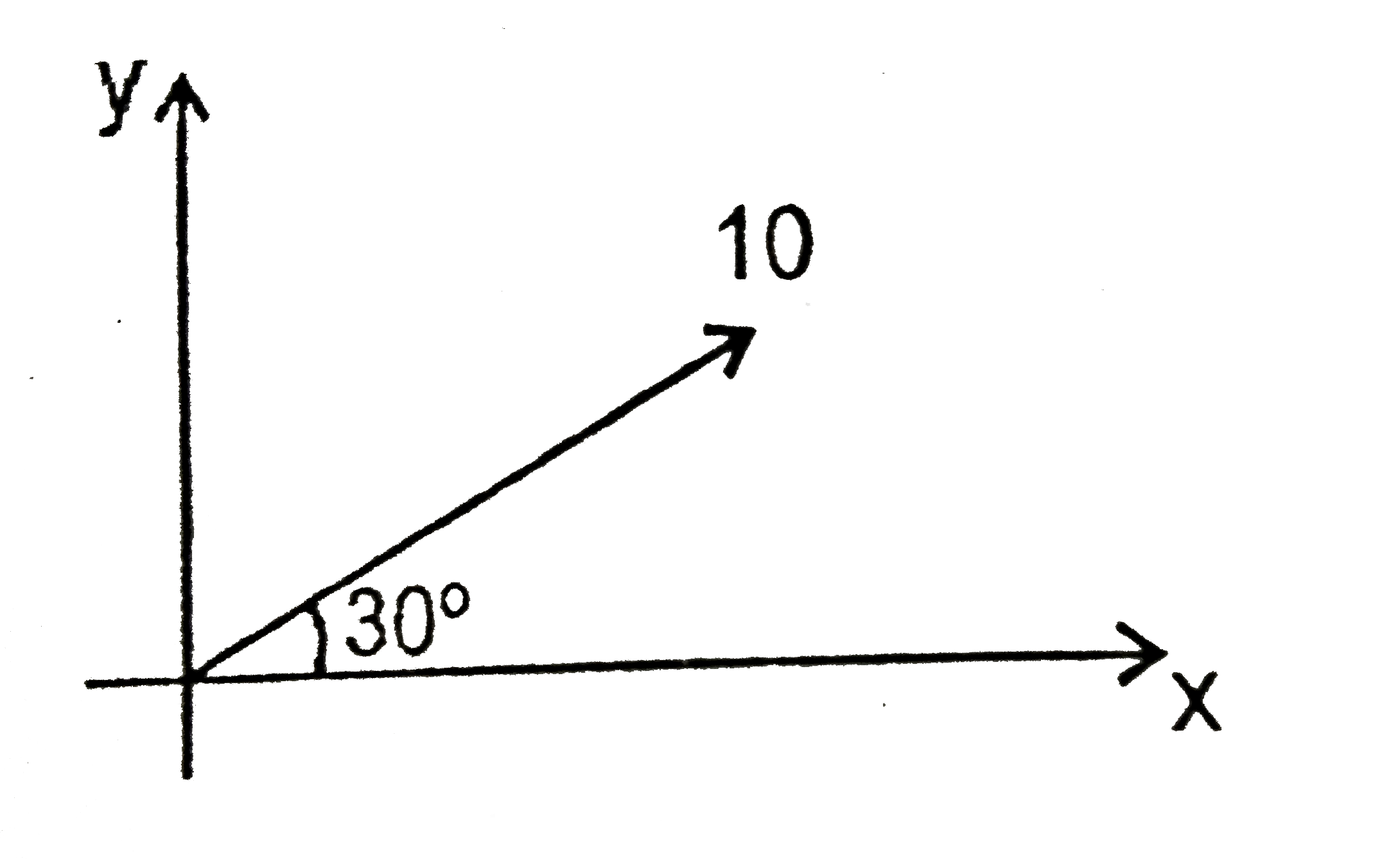
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 16 physics|8 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 17|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise DPP NO. 14 PHYSICS|10 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 15
- A particle travels according to the equation x=at^(3),y=bt^(3). The eq...
Text Solution
|
- The velocity at the maximum height of a projectile is half of its velo...
Text Solution
|
- A ball whose kinetic energy is E , is projected at an angle of 45(@) t...
Text Solution
|
- A particle is projected from a horizontal floor with speed 10(m)/(s) a...
Text Solution
|
- A body is projected with a speed (u) at an angle to the horizontal to ...
Text Solution
|
- Ratio of the ranges of the bullets fired from a gun ( of constant muzz...
Text Solution
|
- A particle is projected with a speed 10sqrt(2) making an angle 45^(@) ...
Text Solution
|
- A particle has initial velocity vec(v)=3hat(i)+4hat(j) and a constant ...
Text Solution
|