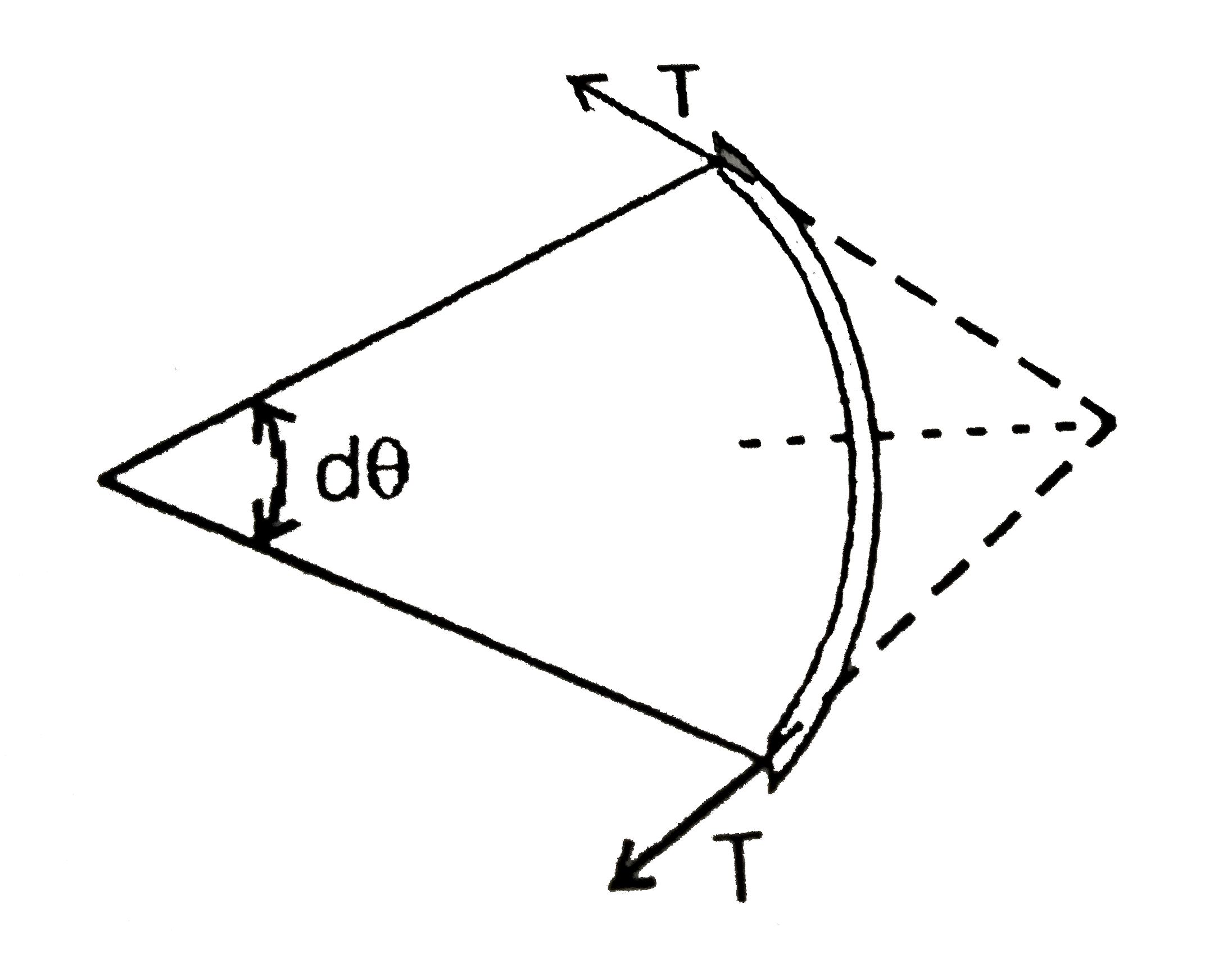
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise DPP 55|8 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 56|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 53|5 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 54
- A uniform disc of mass 'm' and radius R is placed on a smooth horizont...
Text Solution
|
- For a two - body sstem in absence of external forces, the kinetic ener...
Text Solution
|
- A ball of mass m=200gm is suspended from a point A by an inextensible...
Text Solution
|
- Two blocks of mass m(1) and m(2) (m(1) lt m(2)) are connected with an ...
Text Solution
|
- The friction coefficient between the horizontal surface and each of th...
Text Solution
|
- A ring of radius R is made of a thin wire of material of density rho h...
Text Solution
|
- A ring of radius R is made of a thin wire of material of density rho h...
Text Solution
|
- A ring of radius R is made of a thin wire of material of density rho h...
Text Solution
|